【题目】等腰三角形一腰上的高与另一腰的夹角为30°,则它的顶角为 .
参考答案:
【答案】60°或120°
【解析】解:当高在三角形内部时,顶角是120°; 当高在三角形外部时,顶角是60°.
所以答案是:60°或120°.
【考点精析】关于本题考查的等腰三角形的性质,需要了解等腰三角形的两个底角相等(简称:等边对等角)才能得出正确答案.
-
科目: 来源: 题型:
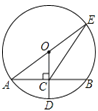
查看答案和解析>>【题目】如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则sin∠ECB为( )
A、
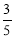 B、
B、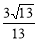 C、
C、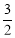 D、
D、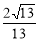
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的正方形网格内有一直角坐标系,其中,A点为(-3,0),B点为(-1,2)

(1)C点的坐标为 ;
(2)依次连接ABC得到三角形,将三角形ABC先向右移动3个单位再向下移动2个单位,得到三角形A'B'C',请在图中作出平移后的图形,并写出三个顶点A'、B' 及C' 的坐标;
(3)连接C'C、B'B,直接写出四边形CC' B'B的面积。
-
科目: 来源: 题型:
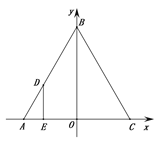
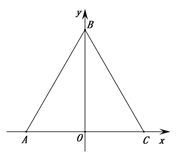
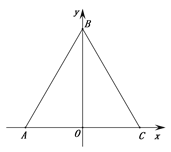
查看答案和解析>>【题目】如图,等边△ABC的边AC在x轴上,AC中点O为坐标原点,已知C(2,0),动点D从A出发沿线段AB向终点B运动,速度为2个单位长度/秒,运动时间为t,过点D作DE⊥AC,垂足为E.
(1)当OD⊥AB时,求E点坐标.
(2)过E做EF⊥BC,垂足为F,过F作FG⊥AB,垂足为G,请用含t的式子表示线段DG的长度.
(3)在(2)的条件下,作点C关于EF的对称点H,连接HG并延长交直线DE于点Q,当t为何值时,HQ=EQ,并求出此时DG的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】改写命题“对角线互相平分的四边形是平行四边形”:如果__________,那么_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】反比例函数的图象如图所示,以下结论正确的是( )
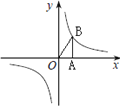
①常数m<1;
②y随x的增大而减小;
③若A为x轴上一点,B为反比例函数上一点,则S△ABC=
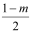 ;
;④若P(x,y)在图象上,则P′(-x,-y)也在图象上.
A.①②③ B.①③④ C.①②③④ D.①④
-
科目: 来源: 题型:
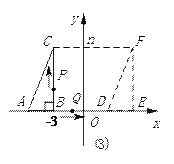
查看答案和解析>>【题目】(12分)如图,直角三角形的顶点A、B在x轴上,ABC=90 ,BC//y轴,且C点在第二象限,B点为(-3,0),将直角三角形ABC沿x轴水平向右平移m个单位,得到对应的直角三角形DEF,其中点A、B、C分别对应点D、E、F,求:
(1)用含m的式子表示E点坐标及AD的长度;
(2)若C点为(-3,n),设四边形BEFC的周长为y,试用含m、n的式子表示周长y;
(3)在(2)的条件下,点P和点Q分别以1个单位/秒,2个单位/秒的速度同时从B点出发,其中,P点沿B→C→F→E→B的方向运动,Q点沿B→E→F→C→B的方向运动,相遇时则停止运动。当P点到达C点时,Q点恰到达E点;从B点出发起,6秒后P点与Q点相遇停止了运动,求四边形ADFC的面积。

相关试题

