Question

【题目】在△ABC纸片中，∠ACB=90°，AC=6，BC=8，沿过其中一个顶点的直线把△ABC剪开，若剪得的两个三角形中仅有一个是等腰三角形，那么这个等腰三角形的面积不可能是（ ）
A.14.4
B.19.2
C.18.75
D.17

Answer 1

【答案】D
【解析】解：在Rt△ABC中，∠ACB=90°，AC=6，BC=8， ∴AB= =10，S△ABC= ACBC=24．
沿过其中一个顶点的直线把△ABC剪开，若剪得的两个三角形中仅有一个是等腰三角形，有四种情况：①当AC=AP=6时，如图1所示，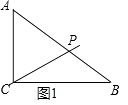

S等腰△ACP= S△ABC= ×24=14.4；②当BC=BP=8时，如图2所示，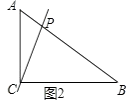

S等腰△BCP= S△ABC= ×24=19.2；③当PA=PB时，如图3所示，

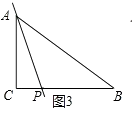
AC2+CP2=PA2 ， 即62+（8﹣PB）2=PB2 ，
解得：PB= ，
∴S等腰△PAB= PBAC= × ×6= =18.75；④当CA=CP=6时，如图4所示，

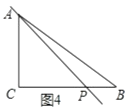
S等腰△CAP= CACP= ×6×6=18．
综上所述：等腰三角形的面积可能为14.4、19.2、18.75或18．
故选D．
【考点精析】本题主要考查了等腰三角形的性质和勾股定理的概念的相关知识点，需要掌握等腰三角形的两个底角相等（简称：等边对等角）；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题．