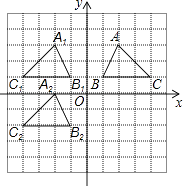
【题目】如图,已知A(2,3)、B(1,1)、C(4,1)是平面直角坐标系中的三点.
(1)①请画出△ABC关于y轴对称的△A1B1C1;
②画出△A1B1C1向下平移3个单位得到的△A2B2C2;
(2)若△ABC中有一点P坐标为(x,y),请直接写出经过以上变换后△A2B2C2中点P的对应点P2的坐标.
参考答案:
【答案】
(1)①解:如图所示:△A1B1C1,即为所求;
②解:如图所示:△A2B2C2,即为所求;
(2)
根据题意可得:P的对应点P2的坐标为:(﹣x,y﹣3).
【解析】(1)①根据轴对称图形的性质得出对应点位置,进而得出答案;
②利用平移的性质得出对应点位置进而得出答案;
(2)利用图象变换规律进而得出对应点坐标变化.
【考点精析】本题主要考查了作轴对称图形的相关知识点,需要掌握画对称轴图形的方法:①标出关键点②数方格,标出对称点③依次连线才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC纸片中,∠ACB=90°,AC=6,BC=8,沿过其中一个顶点的直线把△ABC剪开,若剪得的两个三角形中仅有一个是等腰三角形,那么这个等腰三角形的面积不可能是( )
A.14.4
B.19.2
C.18.75
D.17 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是线段AB上一点,AB=4cm,AO=1cm,若线段AB绕点O顺时针旋转120°到线段A′B′的位置,则线段AB在旋转过程中扫过的图形的面积为 cm2 . (结果保留π)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠BAC=60°,AC与BC交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是 . (把所有正确结论的序号都填在横线上) ①OG=
 AB;
AB;
②与△EGD全等的三角形共有5个;
③S四边形CDGF>S△ABF;
④由点A、B、D、E构成的四边形是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
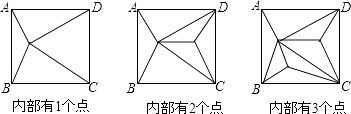
(1)填写如表:正方形ABCD内点的个数
1
2
3
4
…
n
分割成的三角形的个数
4
6
…
(2)如果原正方形被分割成2016个三角形,此时正方形ABCD内部有多少个点?
(3)上述条件下,正方形又能否被分割成2017个三角形?若能,此时正方形ABCD内部有多少个点?若不能,请说明理由.
(4)综上结论,你有什么发现?(写出一条即可) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从点A看一山坡上的电线杆PQ,观测点P的仰角是45°,向前走6m到达B点,测得顶端点P和杆底端点Q的仰角分别是60°和30°,求该电线杆PQ的高度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,正比例函数y=ax的图象与反比例函数y=
 的图象交于点A(3,2)
的图象交于点A(3,2) 
(1)试确定上述正比例函数和反比例函数的表达式;
(2)根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值?
(3)点M(m,n)是反比例函数图象上的一动点,其中0<m<3,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.当四边形OADM的面积为6时,请判断线段BM与DM的大小关系,并说明理由.
相关试题

