【题目】已知A,B两地相距80km,甲,乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车.图中DE,OC分别表示甲,乙离开A地的路程s(km)与时间t(h)的函数关系,根据图象得出的下列信息错误的是( )
A.乙到达B地时甲距A地120km.
B.乙出发1.8小时被甲追上.
C.甲,乙相距20km时,t为2.4h.
D.甲的速度是乙的速度的 ![]() 倍.
倍.
参考答案:
【答案】C
【解析】解:A.直线OC表示乙行驶的过程,乙到达B地时,t=3h,此时,表示甲的DE的直线刚好是在E点,故A正确;
B.设甲函数解析式为y=kx+b,
∵函数图象经过点(1,0),(3,120),
∴ ![]()
解得 ![]()
∴y=60x-60,
乙函数图象为y=kx,则3k=80,解得k= ![]() ,∴y=
,∴y= ![]() x,
x,
联立  解得
解得 ![]() .
.
故B正确;
C.当t<1时,乙离A地20km时, ![]() x=20,解得x=
x=20,解得x= ![]() (h);
(h);
当1<t<3时,60x-60- ![]() x=±20,解得x=2.4或1.2(h),故C错误;
x=±20,解得x=2.4或1.2(h),故C错误;
D.由甲函数y=60x-60得甲的速度为60km/h,由乙函数y= ![]() x得乙的速度为
x得乙的速度为 ![]() km/h,则60÷
km/h,则60÷ ![]() =
= ![]() .
.
A.当t=3时,乙到达B地,甲到达离A地120km的地方;
B.运用待定系数法分别求出甲函数和乙函数,求出它们的交点即可得到答案;
C.有三种情况:一是甲还未出发时,乙行驶到一定时间离A地相距20km;二是甲出发后与乙相距20km,还未相遇;三是相遇后.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了能以“更新、更绿、更洁、更宁”的城市形象迎接2011年大运会的召开,深圳市全面实施市容市貌环境提升行动,某工程队承担了一段长1500米的道路绿化工程,施工时有两种绿化方案:
甲方案是绿化1米的道路需要A型花2枝和B型花3枝,成本是22元;
乙方案是绿化1米的道路需要A型花1枝和B型花5枝,成本是25元.
现要求按照乙方案绿化道路的总长度不能少于按甲方案绿化道路的总长度的2倍.
(1)求A型花和B型花每枝的成本分别是多少元?
(2)求当按甲方案绿化的道路总长度为多少米时,所需工程的总成本最少?总成本最少是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,边长为2的正方形ABCD中,E是BA延长线上一点,且AE=AB,点P从点D出发,以每秒1个单位长度沿D→CB向终点B运动,直线EP交AD于点F,过点F作直线FG⊥DE于点G,交AB于点R.
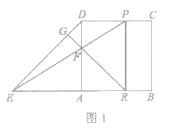

(1)求证:AF=AR;
(2)设点P运动的时间为t秒,求当选t为何值时,四边形PRBC是矩形?
(3)如图2,连接PB,请直线写出使△PRB是等腰三角形时t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C的内接△AOB中,AB=AO=4,tan∠AOB=
 ,抛物线y=ax2+bx经过点A(4,0)与点(-2,6).
,抛物线y=ax2+bx经过点A(4,0)与点(-2,6).
(1)求抛物线的函数解析式;
(2)直线m与C相切于点A,交y轴于点D,求证:AD//OB;
(3)在(2)的条件下,点P在线段OB上,从点O出发向点B运动;同时动点Q在线段DA上,从点D出发向点A运动;点P的速度为每秒1个单位长,点Q的速度为每秒2个单位长,当PQ⊥AD时,求运动时间t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为13,以CD为斜边向外作Rt△CDE,若点A到CE的距离为17,则CE= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】一张宽为6cm的平行四边形纸带ABCD如图1所示,AB=10cm,小
明用这张纸带将底面周长为10cm直三棱柱纸盒的侧面进行包贴(要求包
贴时没有重叠部分). 小明通过操作后发现此类包贴问题可将直三棱柱的
侧面展开进行分析.


(1)若纸带在侧面缠绕三圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则纸带AD的长度为 cm;
(2)若AD=100cm,纸带在侧面缠绕多圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则这个直三棱柱纸盒的高度是cm. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在□ABCD中,对角线AC与BD相交于点O,过点O作一条直线分别交AB,CD于点E,F.

(1)求证:OE=OF;
(2)若AB=6,BC=5,OE=2,求四边形BCFE的周长.
相关试题

