【题目】为了能以“更新、更绿、更洁、更宁”的城市形象迎接2011年大运会的召开,深圳市全面实施市容市貌环境提升行动,某工程队承担了一段长1500米的道路绿化工程,施工时有两种绿化方案:
甲方案是绿化1米的道路需要A型花2枝和B型花3枝,成本是22元;
乙方案是绿化1米的道路需要A型花1枝和B型花5枝,成本是25元.
现要求按照乙方案绿化道路的总长度不能少于按甲方案绿化道路的总长度的2倍.
(1)求A型花和B型花每枝的成本分别是多少元?
(2)求当按甲方案绿化的道路总长度为多少米时,所需工程的总成本最少?总成本最少是多少元?
参考答案:
【答案】
(1)
解:设A型花和B型花每枝的成本分别是x元和y元,根据题意得:
![]()
解得: ![]()
答案:A型花和B型花每枝的成本分别是5元,4元.
(2)
解:设按甲方案绿化的道路总长度为a米,根据题意得:
1500-a≥2a,解得a≤500.
则所需要工程的总成本是
22a+25(1500-a)
=22a+37500-25a
=37500-3a.
当按甲方案绿化的道路总长度为500米时,
所需要工程的总成本最少=37500-3×500=36000(元).
所以当按甲方案绿化的道路总长度为500米时,所需要工程的总成本最少,总成本最少是36000元.
【解析】(1)根据题意运用二元一次方程解答;(2)设按甲方案绿化的道路总长度为a米,根据“现要求按照乙方案绿化道路的总长度不能少于按甲方案绿化道路的总长度的2倍”,即1500-a≥2a,解出a的取值范围;总成本=甲方案每米的成本×米数+乙方案每米的成本×米数,则根据a的取值范围,求总成本的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下列结论:
①△ODC是等边三角形 ②BC=2AB ③∠AOE=135° ④S△AOE=S△COE
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】某课题小组为了解某品牌手机的销售情况,对某专卖店该品牌手机在今年1~4月的销售做了统计,并绘制成如图两幅统计图(如图).


(1)该专卖店1~4月共销售这种品牌的手机台;
(2)请将条形统计图补充完整;
(3)在扇形统计图中,“二月”所在的扇形的圆心角的度数是;
(4)在今年1~4月份中,该专卖店售出该品牌手机的数量的中位数是台. -
科目: 来源: 题型:
查看答案和解析>>【题目】2013年9月23日强台风“天兔”登录深圳,伴随着就是狂风暴雨梧桐山山坡上有一棵与水平面垂直的大树,台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示).已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=3m.


(1)求∠DAC的度数;
(2)求这棵大树折断前的高度?(结果保留根号). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,边长为2的正方形ABCD中,E是BA延长线上一点,且AE=AB,点P从点D出发,以每秒1个单位长度沿D→CB向终点B运动,直线EP交AD于点F,过点F作直线FG⊥DE于点G,交AB于点R.
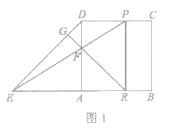

(1)求证:AF=AR;
(2)设点P运动的时间为t秒,求当选t为何值时,四边形PRBC是矩形?
(3)如图2,连接PB,请直线写出使△PRB是等腰三角形时t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C的内接△AOB中,AB=AO=4,tan∠AOB=
 ,抛物线y=ax2+bx经过点A(4,0)与点(-2,6).
,抛物线y=ax2+bx经过点A(4,0)与点(-2,6).
(1)求抛物线的函数解析式;
(2)直线m与C相切于点A,交y轴于点D,求证:AD//OB;
(3)在(2)的条件下,点P在线段OB上,从点O出发向点B运动;同时动点Q在线段DA上,从点D出发向点A运动;点P的速度为每秒1个单位长,点Q的速度为每秒2个单位长,当PQ⊥AD时,求运动时间t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A,B两地相距80km,甲,乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车.图中DE,OC分别表示甲,乙离开A地的路程s(km)与时间t(h)的函数关系,根据图象得出的下列信息错误的是( )

A.乙到达B地时甲距A地120km.
B.乙出发1.8小时被甲追上.
C.甲,乙相距20km时,t为2.4h.
D.甲的速度是乙的速度的 倍.
倍.
相关试题

