【题目】如图,为了测量某棵树的高度,小明用长为2m的竹竿作测量工具,移动竹竿,使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距5m,与树相距10m,则树的高度为( )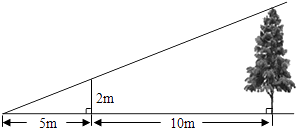
A.5m
B.6m
C.7m
D.8m
参考答案:
【答案】B
【解析】解:如图所示:
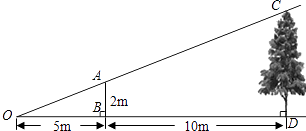
∵AB⊥OD,CD⊥OD,
∴AB∥CD,
∴△OAB∽△OCD,
∴ ![]() ,
,
即 ![]() ,
,
解得:CD=6(米);
即树的高度为6m;
所以答案是:B.
【考点精析】认真审题,首先需要了解相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方),还要掌握相似三角形的应用(测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了更好地开展球类运动,体育组决定用1600元购进足球8个和篮球14个,并且篮球的单价比足球的单价多20元,请解答下列问题:
(1)求出足球和篮球的单价;
(2)若学校欲用不超过3240元,且不少于3200元再次购进两种球50个,求出有哪几种购买方案?
(3)在(2)的条件下,若已知足球的进价为50元,篮球的进价为65元,则在第二次购买方案中,哪种方案商家获利最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC为等边三角形,点D为直线BC上一动点(点D不与点B,点C重合)。以AD为边作等边三角形ADE,连接CE。

(1)如图(1),当点D在边BC上时。
①求证:△ABD≌△ACE;
②直接判断结论BC=DC+CE是否成立(不需证明);
(2)如图2,当点D在边BC的延长线上时,其他条件不变,请写出BC,DC,CE之间存在的数量关系,并写出证明过程。
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解题:定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位.那么形如a+bi(a,b为实数)的数就叫做复数,a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.例如计算:(2+i)+(3-4i)=5-3i.
(1)填空:i3=_____,i4="_______";
(2)计算:①
 ;②
;② ;
;(3)若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:
已知:(x+y)+3i=(1-x)-yi,(x,y为实数),求x,y的值.
(4)试一试:请利用以前学习的有关知识将
 化简成a+bi的形式
化简成a+bi的形式 -
科目: 来源: 题型:
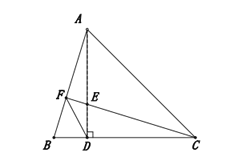
查看答案和解析>>【题目】在
 中,
中,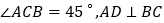 垂足为
垂足为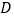 ,点
,点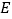 在
在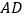 上,
上,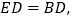 连接
连接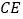 并延长交
并延长交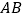 于点
于点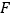 ,连接
,连接 .
.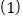 求证:
求证: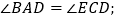
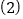 求证:
求证: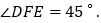
-
科目: 来源: 题型:
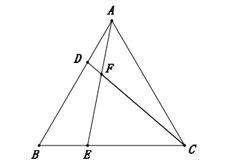
查看答案和解析>>【题目】如图,在等边
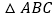 中,点
中,点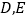 分别在边
分别在边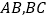 上,
上,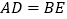 ,线段
,线段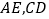 交于点
交于点
 求证:
求证: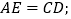
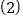 连接
连接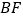 ,当
,当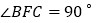 时,求证:
时,求证: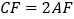 .
.
-
科目: 来源: 题型:
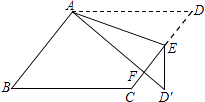
查看答案和解析>>【题目】如图,在ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为 .
相关试题

