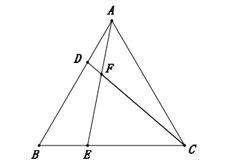
【题目】如图,在等边![]() 中,点
中,点![]() 分别在边
分别在边![]() 上,
上,![]() ,线段
,线段![]() 交于点
交于点![]()
![]() 求证:
求证:![]()
![]() 连接
连接![]() ,当
,当![]() 时,求证:
时,求证:![]() .
.
参考答案:
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)证明△ABE△CAD即可;
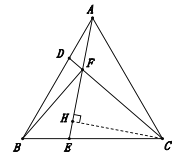
(2)过点C作CH⊥AE,垂足为H,通过证明△BFC△CHA,得到CF=AH,再证明∠FCH=30°,由30°角所对直角边等于斜边的一半,得到CF=2FH,进而可以得到AF=FH,即可得到结论.
(1)∵△ABC等边三角形ABC中,∴∠B=∠BCA=∠CAB=60°,AB=CA=BC.
在△ABE和△CAD中,∵BE=AD,∠B=∠CAB,AB=CA,∴△ABE△CAD,∴AE=CD;
(2)过点C作CH⊥AE,垂足为H,∴∠CHA=90°,∴∠BFC=90°,∠BFC=∠CHA.
∵△ABE△CAD,∴∠BAE=∠ACD.
∵∠CAB-∠BAE=∠BCA-∠ACD,即∠CAE=∠BCD.
在△BFC和△CHA中,∵∠BFC=∠CHA,∠BCD=∠CAE,BC=CA,∴△BFC△CHA,∴CF=AH.
∵∠CFE=∠CAE+∠ACD =∠CAE+∠BAE=∠CAB=60°.
∴∠FCH=180°-∠CHA-∠CFE =180°-90°-60°=30°,∴CF=2FH,∴AH=2FH,即AF+FH=2FH,∴AF=FH,∴CF=2AF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解题:定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位.那么形如a+bi(a,b为实数)的数就叫做复数,a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.例如计算:(2+i)+(3-4i)=5-3i.
(1)填空:i3=_____,i4="_______";
(2)计算:①
 ;②
;② ;
;(3)若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:
已知:(x+y)+3i=(1-x)-yi,(x,y为实数),求x,y的值.
(4)试一试:请利用以前学习的有关知识将
 化简成a+bi的形式
化简成a+bi的形式 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了测量某棵树的高度,小明用长为2m的竹竿作测量工具,移动竹竿,使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距5m,与树相距10m,则树的高度为( )
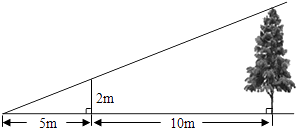
A.5m
B.6m
C.7m
D.8m -
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, 垂足为
垂足为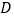 ,点
,点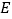 在
在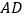 上,
上,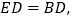 连接
连接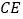 并延长交
并延长交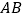 于点
于点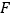 ,连接
,连接 .
.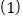 求证:
求证: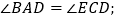
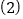 求证:
求证: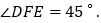
-
科目: 来源: 题型:
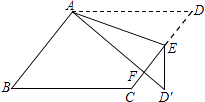
查看答案和解析>>【题目】如图,在ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为 .
-
科目: 来源: 题型:
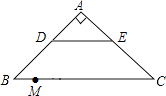
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,长方形
 中,
中,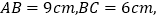 点
点 从点
从点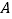 出发,沿
出发,沿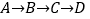 运动,同时,点
运动,同时,点 从点
从点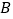 出发,沿
出发,沿 运动,当点
运动,当点 到达点
到达点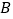 时,点
时,点 恰好到达点
恰好到达点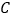 ,已知点
,已知点 每秒比点
每秒比点 每秒多运动
每秒多运动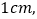 当其中一点到达
当其中一点到达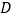 时,另一点停止运动.
时,另一点停止运动.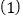 求
求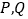 两点的运动速度;
两点的运动速度;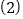 当其中一点到达点
当其中一点到达点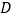 时,另一点距离
时,另一点距离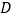 点
点 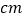 (直接写答案);
(直接写答案);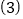 设点
设点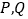 的运动时间为
的运动时间为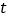 秒
秒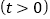 ,请用含
,请用含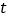 的代数式表示
的代数式表示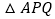 的面积
的面积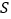 ,并写出
,并写出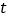 的取值范围.
的取值范围.
相关试题

