【题目】对于平面直角坐标系xOy中的点P,给出如下定义:记点P到x轴的距离为![]() ,到y轴的距离为
,到y轴的距离为![]() ,若
,若![]() ,则称
,则称![]() 为点P的最大距离;若
为点P的最大距离;若![]() ,则称
,则称![]() 为点P的最大距离.
为点P的最大距离.
例如:点P(![]() ,
, ![]() )到到x轴的距离为4,到y轴的距离为3,因为3<4,所以点P的最大距离为
)到到x轴的距离为4,到y轴的距离为3,因为3<4,所以点P的最大距离为![]() .
.
(1)①点A(2, ![]() )的最大距离为________;
)的最大距离为________;
②若点B(![]() ,
, ![]() )的最大距离为
)的最大距离为![]() ,则
,则![]() 的值为________;
的值为________;
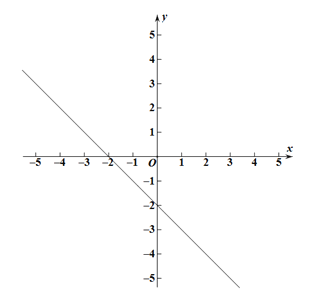
(2)若点C在直线![]() 上,且点C的最大距离为
上,且点C的最大距离为![]() ,求点C的坐标;
,求点C的坐标;
(3)若⊙O上存在点M,使点M的最大距离为![]() ,直接写出⊙O的半径r的取值范围.
,直接写出⊙O的半径r的取值范围.

参考答案:
【答案】(1)①5;②±5;(2)点C(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() );(3)
);(3)![]() .
.
【解析】试题分析:(1)①直接根据“最大距离”的定义,其最小距离为“最大距离”;
②点B(a,2)到x轴的距离为2,且其“最大距离”为5,所以a=±5;
(2)根据点C的“最大距离”为5,可得x=±5或y=±5,代入可得结果;
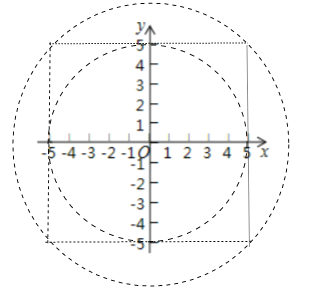
(3)如图,观察图象可知:当⊙O于直线x=5,直线x=﹣5,直线y=5,直线y=﹣5有交点时,⊙O上存在点M,使点M的最大距离为5.
试题解析:解:(1)①∵点A(2,﹣5)到x轴的距离为5,到y轴的距离为2.∵2<5,∴点A的“最大距离”为5.
②∵点B(a,2)的“最大距离”为5,∴a=±5;故答案为:5,±5.
(2)设点C的坐标(x,y),∵点C的“最大距离”为5,∴x=±5或y=±5,当x=5时,y=﹣7,当x=﹣5时,y=3,当y=5时,x=﹣7,当y=﹣5时,x=3,∴点C(﹣5,3)或(3,﹣5).
(3)如图,观察图象可知:当⊙O于直线x=5,直线x=﹣5,直线y=5,直线y=﹣5有交点时,⊙O上存在点M,使点M的最大距离为5,∴5≤r≤![]() .
.
-
科目: 来源: 题型:
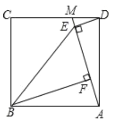
查看答案和解析>>【题目】如图,点M是正方形ABCD边CD上一点,连接AM,作DE⊥AM于点E,作BF⊥AM于点F,连接BE. 若AF=1,四边形ABED的面积为6,则BF的长为( )
A.2B.3C.
 D.
D.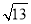
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:
①
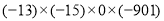
② -10 - (-31)
③1÷(﹣
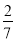 )×
)×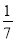 ;
;④(-2)2×5+(-2)3÷4
⑤
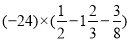
(2)比较大小
①1.5与4 ②2与-7
③
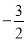 与
与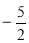 ④
④ 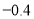 与
与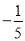
(3)用简便方法计算:
①
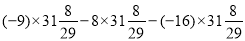
②
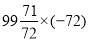
-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)在数轴上表示下列各数:0,–2.5,
 ,–2,+5,
,–2,+5, .
.
(2)将上列各数用“<”连接起来:___________ _____________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读第①小题的计算方法,再计算第②小题.
①–5
 +(–9
+(–9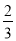 )+17
)+17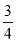 +(–3
+(–3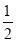 )
)解:原式=[(–5)+(–
 )]+[(–9)+(–
)]+[(–9)+(–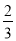 )]+(17+
)]+(17+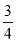 )+[(–3+(–
)+[(–3+(–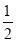 )]
)]=[(–5)+(–9)+(–3)+17]+[(–
 )+(–
)+(–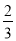 )+(–
)+(–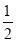 )+
)+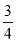 ]
]=0+(–1
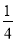 )
)=–1
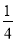 .
.上述这种方法叫做拆项法.灵活运用加法的交换律、结合律可使运算简便.
②仿照上面的方法计算:(﹣2000
 )+(﹣1999
)+(﹣1999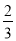 )+4000
)+4000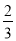 +(﹣1
+(﹣1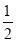 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】下面是“用三角板画圆的切线”的画图过程.
如图1,已知圆上一点A,画过A点的圆的切线.


画法:(1)如图2,将三角板的直角顶点放在圆上任一点C(与点A不重合)处,使其一直角边经过点A,另一条直角边与圆交于B点,连接AB;
(2)如图3,将三角板的直角顶点与点A重合,使一条直角边经过点B,画出另一条直角边所在的直线AD.
所以直线AD就是过点A的圆的切线.
请回答:该画图的依据是_______________________________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】生活与数学
日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
(1)姆同学在某月的日历上圈出2×2个数,正方形的方框内的四个数的和是48,那么这四个数是_______.
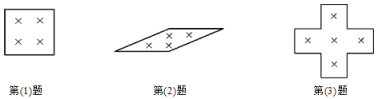
(2)丽也在上面的日历上圈出2×2个数,斜框内的四个数的和是46,则它们分别是_____.
(3)莉也在日历上圈出5个数,呈十字框形,它们的和是55,则中间的数是______.
(4)某月有5个星期日的和是75,则这个月中最后一个星期日是______号?
相关试题

