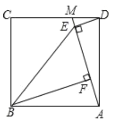
【题目】如图,点M是正方形ABCD边CD上一点,连接AM,作DE⊥AM于点E,作BF⊥AM于点F,连接BE. 若AF=1,四边形ABED的面积为6,则BF的长为( )
A.2B.3C.![]() D.
D.![]()
参考答案:
【答案】B
【解析】
先证明ΔABF≌ΔDAE得到BF=AE,设BF=x,则AE=x,DE=AF=1,利用四边形ABED的面积=![]() 得
得![]() ,解之即可求得BF的长.
,解之即可求得BF的长.
∵四边形ABCD是正方形,
∴BA=AD,∠BAD=90,
∴∠DAE+∠BAF=90,
∵BF⊥AM,DE⊥AM,
∴∠AFB=∠DEA=90,
∴∠ABF+∠BAF=90,
∴∠ABF=∠DAE,
在ΔABF和ΔDAE中
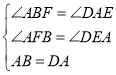
∴ΔABF≌ΔDAE(AAS),
∴BF=AE,DE=AF=1
设BF=x,则AF=x,
由四边形ABED的面积为6得:
![]() ,即
,即![]() ,
,
解得:![]() (舍去),
(舍去),
∴BF=3,
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数分别填入相应的集合里:0,-3.14,-(-10),
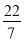 ,-4
,-4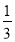 ,15%,
,15%, ,0.3,
,0.3, ,10.01001000100001…
,10.01001000100001…非负整数集合:{ …}
正分数集合:{ …}
无理数集合:{ …}
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 两点在数轴上对应的数分别为
两点在数轴上对应的数分别为 ,且点A在点B的左侧,
,且点A在点B的左侧,
(1)求出a,b的值;
(2)现有一只蚂蚁P从点A出发,以每秒3个单位长度的速度向右运动,同时另一只蚂蚁Q从点B出发,以每秒2个单位长度的速度向右运动.
①两只蚂蚁经过多长时间相遇?
②设两只蚂蚁在数轴上的点C处相遇,求点C对应的数;
③经过多长时间,两只蚂蚁在数轴上相距20个单位长度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,A(a,b),B(c,0)是x轴正半轴上一点,∠ABO=30°,若
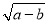 与|2﹣a|互为相反数.
与|2﹣a|互为相反数.
(1)求c的值;
(2)如图2,AC⊥AB交x轴于C,以AC为边的正方形ACDE的对角线AD交x轴于F.
①求证:BE=2OC;
②记BF2﹣OF2=m,OC2=n,求
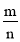 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:
①
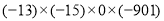
② -10 - (-31)
③1÷(﹣
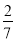 )×
)×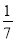 ;
;④(-2)2×5+(-2)3÷4
⑤
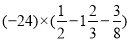
(2)比较大小
①1.5与4 ②2与-7
③
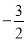 与
与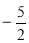 ④
④ 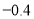 与
与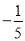
(3)用简便方法计算:
①
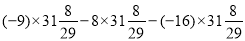
②
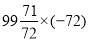
-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)在数轴上表示下列各数:0,–2.5,
 ,–2,+5,
,–2,+5, .
.
(2)将上列各数用“<”连接起来:___________ _____________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面直角坐标系xOy中的点P,给出如下定义:记点P到x轴的距离为
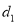 ,到y轴的距离为
,到y轴的距离为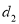 ,若
,若 ,则称
,则称 为点P的最大距离;若
为点P的最大距离;若 ,则称
,则称 为点P的最大距离.
为点P的最大距离.例如:点P(
 ,
,  )到到x轴的距离为4,到y轴的距离为3,因为3<4,所以点P的最大距离为
)到到x轴的距离为4,到y轴的距离为3,因为3<4,所以点P的最大距离为 .
.(1)①点A(2,
 )的最大距离为________;
)的最大距离为________;②若点B(
 ,
,  )的最大距离为
)的最大距离为 ,则
,则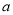 的值为________;
的值为________;(2)若点C在直线
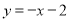 上,且点C的最大距离为
上,且点C的最大距离为 ,求点C的坐标;
,求点C的坐标;
(3)若⊙O上存在点M,使点M的最大距离为
 ,直接写出⊙O的半径r的取值范围.
,直接写出⊙O的半径r的取值范围.
相关试题

