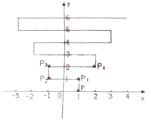
【题目】如图,在平面直角坐标系上有个点![]() ,点
,点![]() 第1次向上跳动1个单位至点
第1次向上跳动1个单位至点![]() ,紧接着第2次向左跳动2个单位至点
,紧接着第2次向左跳动2个单位至点![]() ,第3次向上跳动1个单位到达
,第3次向上跳动1个单位到达![]() ,第4次向右跳动3个单位到达
,第4次向右跳动3个单位到达![]() ,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点
,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点![]() 的坐标为( ).
的坐标为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】C
【解析】
设第n次跳动至点Pn,根据部分点An坐标的变化找出变化规律“P4n(n+1,2n),P4n+1(n+1,2n+1),P4n+2(n1,2n+1),P4n+3(n1,2n+2)”,依此规律结合2019=504×4+3即可得出点P2019的坐标.
设第n次跳动至点Pn,
观察发现:P(1,0),P1(1,1),P2(1,1),P3(1,2),P4(2,2),P5(2,3),P6(2,3),P7(2,4),P8(3,4),P9(3,5),…,
∴P4n(n+1,2n),P4n+1(n+1,2n+1),P4n+2(n1,2n+1),P4n+3(n1,2n+2)(n为自然数).
∵2019=504×4+3,
∴P2019(-504-1,504×2+2),即![]() .
.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
 x2﹣
x2﹣  x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π). -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=x3﹣3x的图象如图所示,则以下关于该函数图象及其性质的描述正确的是( )
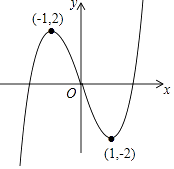
A.函数最大值为2
B.函数图象最低点为(1,﹣2)
C.函数图象关于原点对称
D.函数图象关于y轴对称 -
科目: 来源: 题型:
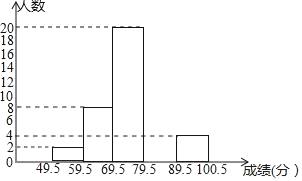
查看答案和解析>>【题目】某校数学兴趣小组成员刘明对本班上学期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析(每个人的成绩各不相同),绘制成如下下频数分布表和频数分布直方图,请你根据图表提供的信息,解答下列问题:
(1)频数、频率分布表中a= ,b= ,c= ;
(2)补全频数分布直方图;
(3)如果要画该班上学期期末考试数学成绩的扇形统计图,那么分数在69.5﹣79.5之间的扇形圆心角的度数是 ;
(4)张亮同学成绩为79分,他说:“我们班上比我成绩高的人还有
 ,我要继续努力.”他的说法正确吗?请说明理由.
,我要继续努力.”他的说法正确吗?请说明理由.分组
49.5~59.5
59.5~69.5
69.5~79.5
79.5~89.5
89.5~100.5
合计
频数
2
8
20
a
4
c
频率
0.04
b
0.40
0.32
0.08
1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如下图, AB∥CD,点E,F分别为AB,CD上一点.
(1) 在AB,CD之间有一点M(点M不在线段EF上),连接ME,MF,试探究∠AEM,∠EMF,∠MFC之间有怎样的数量关系. 请补全图形,并在图形下面写出相应的数量关系,选其中一个进行证明.

(2)如下图,在AB,CD之间有两点M,N,连接ME,MN,NF,请选择一个图形写出∠AEM,∠EMN,∠MNF,∠NFC 存在的数量关系(不需证明).

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了倡导绿色出行,某市政府2016年投资了320万元,首期建成120个公共自行车站点,配置2500辆公共自行车,2017年又投资了104万元新建了40个公共自行车站点,配置800辆公共自行车.
(1)请问每个站点的造价和公共自行车的单价分别是多少万元?
(2)若到2020年该市政府将再建造
 个新公共自行车站点和配置
个新公共自行车站点和配置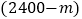 辆公共自行车,并且公共自行车数量不超过新公共自行车站点数量的23倍,并且再建造的新公共自行车站点不超过102个,市政府共有几种选择方案,哪种方案市政府投入的资金最少?(注:从2016年起至2020年,每个站点的造价和公共自行车的单价每年都保持不变)
辆公共自行车,并且公共自行车数量不超过新公共自行车站点数量的23倍,并且再建造的新公共自行车站点不超过102个,市政府共有几种选择方案,哪种方案市政府投入的资金最少?(注:从2016年起至2020年,每个站点的造价和公共自行车的单价每年都保持不变) -
科目: 来源: 题型:
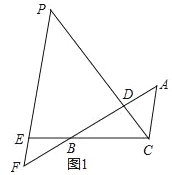
查看答案和解析>>【题目】如图1,△ABC中,点D在线段AB上,点E在线段CB延长线上,且BE=CD,EP∥AC交直线CD于点P,交直线AB于点F,∠ADP=∠ACB.
(1)图1中是否存在与AC相等的线段?若存在,请找出,并加以证明,若不存在,说明理由;
(2)若将“点D在线段AB上,点E在线段CB延长线上”改为“点D在线段BA延长线上,点E在线段BC延长线上”,其他条件不变(如图2).当∠ABC=90°,∠BAC=60°,AB=2时,求线段PE的长.

相关试题

