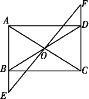
【题目】如图所示,在矩形ABCD中,O是AC与BD的交点,过点O的直线EF与AB,CD的延长线分别交于点E,F.
(1)求证:△BOE≌△DOF;
(2)当EF与AC满足什么条件时,四边形AECF是菱形?并证明你的结论.
参考答案:
【答案】(1)证明:∵四边形ABCD是矩形,AC和BD交于点O
∴AB∥CD; OB=OD
∴∠OEB=∠OFD
∵∠BOE=∠DOF
∴△BOE≌△DOF
(2)解:当EF与AC垂直的时候四边形AECF是菱形。
证明如下:
∵△BOE≌△DOF
∴ BE="DF"
∵ AB=CD
∴AE=CF且AE∥CF
又∵EF⊥AC
∴ 四边形AECF是菱形
【解析】
(1)由矩形的性质:OB=OD,AE∥CF证得△BOE≌△DOF;
(2)当EF⊥AC时,四边形AECF是菱形.根据已知条件可证明四边形AECF是平行四边形,当EF⊥AC,可根据对角线互相垂直的平行四边形是菱形判定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
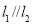 ,直线
,直线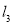 交
交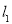 于
于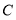 点,交
点,交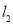 于
于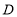 点,
点, 是线段
是线段 上的一个动点,
上的一个动点,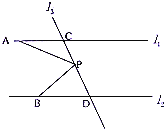
(1)若
 点在线段
点在线段 (
(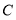 、
、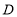 两点除外)上运动,问
两点除外)上运动,问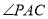 ,
,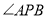 ,
,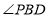 之间的关系是什么?这种关系是否变化?
之间的关系是什么?这种关系是否变化?(2)若
 点在线段
点在线段 之外时,
之外时,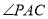 ,
,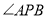 ,
,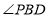 之间的关系怎样?说明理由
之间的关系怎样?说明理由 -
科目: 来源: 题型:
查看答案和解析>>【题目】在东西向的马路上有一个巡岗亭A,巡岗员甲从岗亭A出发以13km/h速度匀速来回巡逻,如果规定向东巡逻为正,向西巡逻为负,巡逻情况记录如下:(单位:千米)
第一次
第二次
第三次
第四次
第五次
第六次
第七次
4
-5
3
-4
-3
6
-1
(1)求第六次结束时甲的位置(在岗亭A的东边还是西边?距离多远?)
(2)在第几次结束时距岗亭A最远?距离A多远?
(3)巡逻过程中配置无线对讲机,并一直与留守在岗亭A的乙进行通话,问在甲巡逻过程中,甲与乙的保持通话时长共多少小时?
-
科目: 来源: 题型:
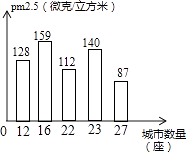
查看答案和解析>>【题目】如图是我校某班同学随机抽取的我国100座城市2017年某天当地pm2.5值的情况的条形统计图,那么本次调查中,PM2.5值的中位数为微克/立方米.
-
科目: 来源: 题型:
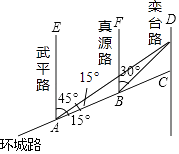
查看答案和解析>>【题目】如图,AC是某市环城路的一段,AE,BF,CD都是南北方向的街道,其与环城路AC的交叉路口分别是A,B,C经测量东方家具城D位于点A的北偏东45°方向,点B的北偏东30°方向上,AB=2km,∠DAC=15°,求C、D之间的距离(结果保留根号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数a,b,c在数轴上的位置如图所示,且表示数a的点、数b的点与原点的距离相等.
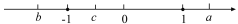
(1)用“<”连接0,a, b, —1
(2)|b-1|+|a-1|=___
(3)化简|a —b|+|a-c|-|b|+|b-c|
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
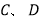 两地各需220吨和280吨化肥,A市有化肥200吨,B市有化肥300吨,刚好可以全部运往
两地各需220吨和280吨化肥,A市有化肥200吨,B市有化肥300吨,刚好可以全部运往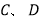 两地,如果从A市运往
两地,如果从A市运往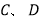 两地运价分别为20元/吨和25元/吨,从B市运往
两地运价分别为20元/吨和25元/吨,从B市运往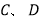 两地运价分别为15元/吨和22元/吨。
两地运价分别为15元/吨和22元/吨。(1)如果A市运往C地的化肥为100吨,则总运费共多少元?
(2)设总运费为
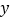 元,如果设A市运往C地的化肥
元,如果设A市运往C地的化肥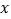 吨,用含
吨,用含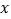 代数式来表示
代数式来表示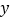 ;
; (3)按照(2)问的要求,猜想
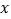 为多少时,总的运费最少,是多少?
为多少时,总的运费最少,是多少?
相关试题

