【题目】如图,直线AB、CD相交于点O,EO⊥AB,垂足为O,∠EOC:∠AOD=7:11,求∠DOE的度数. 
参考答案:
【答案】解:∵EO⊥AB,
∴∠EOA=90°,
∴∠EOC+∠AOD=90°,
∵∠EOC:∠AOD=7:11,
∴∠AOD=90°× ![]() =55°,
=55°,
∴∠DOE=∠EOA+∠AOD=90°+55°=145°,
答:∠DOE的度数是145°.
【解析】根据垂直定义可得∠EOA=90°,根据对顶角相等可得∠EOC+∠AOD=90°,再根据条件∠EOC:∠AOD=7:11可算出∠AOD的度数,进而可得∠DOE的度数.
【考点精析】解答此题的关键在于理解垂线的性质的相关知识,掌握垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,那么大树CD的高度约为( )(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)
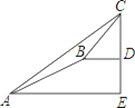
A. 8.1米 B. 17.2米 C. 19.7米 D. 25.5米
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E、F分别是BC、CD边上的点,且∠EAF=45°,对角线BD交AE于点M,交AF于点N.若AB=4
 ,BM=2,则MN的长为_______.
,BM=2,则MN的长为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知代数式ax5+bx3+3x+c,当x=0时,该代数式的值为﹣1.
(1)求c的值;
(2)已知当x=1时,该代数式的值为﹣1,试求a+b+c的值;
(3)已知当x=3时,该代数式的值为9,试求当x=﹣3时该代数式的值;
(4)在第(3)小题的已知条件下,若有3a=5b成立,试比较a+b与c的大小? -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(﹣2,﹣3)所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在同一直线噵路上同起点,同方向同进出发,分别以不同的速度匀速跑步1500米,当甲超出乙200米时,甲停下来等候乙,甲、乙会合后,两人分别以原来的速度继续跑向终点,先到达终点的人在终点休息,在跑步的整个过程中,甲、乙两人的距离y(米)与出发的时间x(秒)之间的关系如图所示,则甲到终点时,乙距离终点______________米。
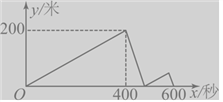
-
科目: 来源: 题型:
查看答案和解析>>【题目】口袋里装有五个大小形状都相同,所标数字不同的小球,小球所标的数字分别是 -3,-2.5,-1,2,3,先随机抽取一个球得到的数字记为k,放回后再抽一个球得到的数字记为b ,则满足条件关于x的一次函数
 的图象不经过第四象限的概率是_________。
的图象不经过第四象限的概率是_________。
相关试题

