【题目】探究题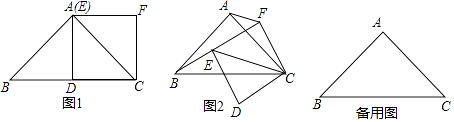
(1)【问题发现】
如图1,在Rt△ABC中,AB=AC=2,∠BAC=90°,点D为BC的中点,以CD为一边作正方形CDEF,点E恰好与点A重合,则线段BE与AF的数量关系为
(2)【拓展研究】
在(1)的条件下,如果正方形CDEF绕点C旋转,连接BE,CE,AF,线段BE与AF的数量关系有无变化?请仅就图2的情形给出证明;
(3)【问题发现】
当正方形CDEF旋转到B,E,F三点共线时候,直接写出线段AF的长.
参考答案:
【答案】
(1)解:BE= ![]() AF
AF
(2)
解:无变化;
如图2,在Rt△ABC中,AB=AC=2,
∴∠ABC=∠ACB=45°,
∴sin∠ABC= ![]() =
= ![]() ,
,
在正方形CDEF中,∠FEC= ![]() ∠FED=45°,
∠FED=45°,
在Rt△CEF中,sin∠FEC= ![]() ,
,
∴ ![]() ,
,
∵∠FCE=∠ACB=45°,
∴∠FCE﹣∠ACE=∠ACB﹣∠ACE,
∴∠FCA=∠ECB,
∴△ACF∽△BCE,
∴ ![]() ,
,
∴BE= ![]() AF,
AF,
∴线段BE与AF的数量关系无变化
(3)
解:当点E在线段AF上时,如图2,
由(1)知,CF=EF=CD= ![]() ,
,
在Rt△BCF中,CF= ![]() ,BC=2
,BC=2 ![]() ,
,
根据勾股定理得,BF= ![]() ,
,
∴BE=BF﹣EF= ![]() ﹣
﹣ ![]() ,
,
由(2)知,BE= ![]() AF,
AF,
∴AF= ![]() ﹣1,
﹣1,
当点E在线段BF的延长线上时,如图3,
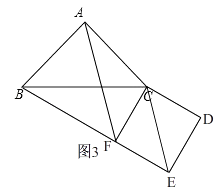
在Rt△ABC中,AB=AC=2,
∴∠ABC=∠ACB=45°,
∴sin∠ABC= ![]() =
= ![]() ,
,
在正方形CDEF中,∠FEC= ![]() ∠FED=45°,
∠FED=45°,
在Rt△CEF中,sin∠FEC= ![]() ,
,
∴ ![]() ,
,
∵∠FCE=∠ACB=45°,
∴∠FCB+∠ACB=∠FCB+∠FCE,
∴∠FCA=∠ECB,
∴△ACF∽△BCE,
∴ ![]() ,
,
∴BE= ![]() AF,
AF,
由(1)知,CF=EF=CD= ![]() ,
,
在Rt△BCF中,CF= ![]() ,BC=2
,BC=2 ![]() ,
,
根据勾股定理得,BF= ![]() ,
,
∴BE=BF+EF= ![]() +
+ ![]() ,
,
由(2)知,BE= ![]() AF,
AF,
∴AF= ![]() +1.
+1.
即:当正方形CDEF旋转到B,E,F三点共线时候,线段AF的长为 ![]() ﹣1或
﹣1或 ![]() +1.
+1.
【解析】解:(1)在Rt△ABC中,AB=AC=2,
根据勾股定理得,BC= ![]() AB=2
AB=2 ![]() ,
,
点D为BC的中点,
∴AD= ![]() BC=
BC= ![]() ,
,
∵四边形CDEF是正方形,
∴AF=EF=AD= ![]() ,
,
∵BE=AB=2,
∴BE= ![]() AF,
AF,
故答案为BE= ![]() AF;
AF;
(1)先利用等腰直角三角形的性质得出AD= ![]() ,再得出BE=AB=2,即可得出结论;(2)先利用三角函数得出
,再得出BE=AB=2,即可得出结论;(2)先利用三角函数得出 ![]() ,同理得出
,同理得出 ![]() ,夹角相等即可得出△ACF∽△BCE,进而得出结论;(3)分两种情况计算,当点E在线段BF上时,如图2,先利用勾股定理求出EF=CF=AD=
,夹角相等即可得出△ACF∽△BCE,进而得出结论;(3)分两种情况计算,当点E在线段BF上时,如图2,先利用勾股定理求出EF=CF=AD= ![]() ,BF=
,BF= ![]() ,即可得出BE=
,即可得出BE= ![]() ﹣
﹣ ![]() ,借助(2)得出的结论,当点E在线段BF的延长线上,同前一种情况一样即可得出结论.
,借助(2)得出的结论,当点E在线段BF的延长线上,同前一种情况一样即可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市在创建全国文明城市过程中,决定购买A,B两种树苗对某路段道路进行绿化改造,已知购买A种树苗8棵,B种树苗3棵,需要950元;若购买A种树苗5棵,B种树苗6棵,则需要800元.
(1)求购买A,B两种树苗每棵各需多少元?
(2)考虑到绿化效果和资金周转,购进A种树苗不能少于50棵,且用于购买这两种树苗的资金不能超过7650元,若购进这两种树苗共100棵,则有哪几种购买方案?
(3)某包工队承包种植任务,若种好一棵A种树苗可获工钱30元,种好一棵B种树苗可获工钱20元,在第(2)问的各种购买方案中,种好这100棵树苗,哪一种购买方案所付的种植工钱最少?最少工钱是多少元? -
科目: 来源: 题型:
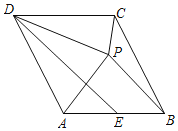
查看答案和解析>>【题目】在菱形ABCD中,
 ,点E为AB边的中点,点P与点A关于DE对称,连接DP、BP、CP,下列结论:
,点E为AB边的中点,点P与点A关于DE对称,连接DP、BP、CP,下列结论: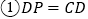 ;
;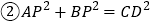 ;
;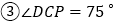 ;
;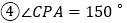 ,其中正确的是
,其中正确的是
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料: 如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2=
 交于A(1,3)和B(﹣3,﹣1)两点.
交于A(1,3)和B(﹣3,﹣1)两点.
观察图象可知:
①当x=﹣3或1时,y1=y2;
②当﹣3<x<0或x>1时,y1>y2 , 即通过观察函数的图象,可以得到不等式ax+b> 的解集.
的解集.
有这样一个问题:求不等式x3+4x2﹣x﹣4>0的解集.
某同学根据学习以上知识的经验,对求不等式x3+4x2﹣x﹣4>0的解集进行了探究.
下面是他的探究过程,请将探究过程补充完整:
将不等式按条件进行转化:
当x=0时,原不等式不成立;
当x>0时,原不等式可以转化为x2+4x﹣1> ;
;
当x<0时,原不等式可以转化为x2+4x﹣1< ;
;
(1)构造函数,画出图象 设y3=x2+4x﹣1,y4= ,在同一坐标系中分别画出这两个函数的图象.
,在同一坐标系中分别画出这两个函数的图象.
双曲线y4= 如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
(2)确定两个函数图象公共点的横坐标 观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为;
(3)借助图象,写出解集 结合(1)的讨论结果,观察两个函数的图象可知:不等式x3+4x2﹣x﹣4>0的解集为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣x﹣4与抛物线y=ax2+bx+c相交于A,B两点,其中A,B两点的横坐标分别为﹣1和﹣4,且抛物线过原点.

(1)求抛物线的解析式;
(2)在坐标轴上是否存在点C,使△ABC为等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)若点P是线段AB上不与A,B重合的动点,过点P作PE∥OA,与抛物线第三象限的部分交于一点E,过点E作EG⊥x轴于点G,交AB于点F,若S△BGF=3S△EFP , 求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们规定运算符号的意义是:当a>b时,ab=a﹣b;当a<b时,ab=a+b.
(1)计算:61= ;(﹣3)2= ;
(2)棍据运算符号的意义且其他运算符号意义不变的条件下,
①计算:﹣14+15×[(﹣
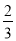 )(﹣
)(﹣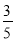 )]﹣(3223)÷(﹣7),
)]﹣(3223)÷(﹣7),②若x,y在数轴上的位置如图所示,
a.填空:x2+1 y(填“>“或“<”):
b.化简:[(x2+x+1)(x+y)]+[(y﹣x2)(y+2)].

-
科目: 来源: 题型:
查看答案和解析>>【题目】为进一步提升企业产品竞争力,某企业加大了科研经费的投入,2016年该企业投入科研经费5000万元,2018年投入科研经费7200万元,假设该企业这两年投入科研经费的年平均增长率相同.
 求这两年该企业投入科研经费的年平均增长率.
求这两年该企业投入科研经费的年平均增长率. 若该企业科研经费的投入还将保持相同的年平均增长率,请你预算2020年该企业投入科研经费多少万元.
若该企业科研经费的投入还将保持相同的年平均增长率,请你预算2020年该企业投入科研经费多少万元.
相关试题

