【题目】我市在创建全国文明城市过程中,决定购买A,B两种树苗对某路段道路进行绿化改造,已知购买A种树苗8棵,B种树苗3棵,需要950元;若购买A种树苗5棵,B种树苗6棵,则需要800元.
(1)求购买A,B两种树苗每棵各需多少元?
(2)考虑到绿化效果和资金周转,购进A种树苗不能少于50棵,且用于购买这两种树苗的资金不能超过7650元,若购进这两种树苗共100棵,则有哪几种购买方案?
(3)某包工队承包种植任务,若种好一棵A种树苗可获工钱30元,种好一棵B种树苗可获工钱20元,在第(2)问的各种购买方案中,种好这100棵树苗,哪一种购买方案所付的种植工钱最少?最少工钱是多少元?
参考答案:
【答案】
(1)解:设购买A种树苗每棵需要x元,B种树苗每棵需要y元,
由已知得: ![]() ,
,
解得: ![]() .
.
答:购买A种树苗每棵需要100元,B种树苗每棵需要50元
(2)解:设购买A种树苗m棵,则购买B种树苗100﹣m棵,
根据已知,得 ![]() ,
,
解得:50≤m≤53.
故有四种购买方案:1、购买A种树苗50棵,B种树苗50棵;2、购买A种树苗51棵,B种树苗49棵;3、购买A种树苗52棵,B种树苗48棵;4、购买A种树苗53棵,B种树苗47棵
(3)解:设种植工钱为W,由已知得:
W=30m+20(100﹣m)=10m+2000,
∴当m=50时,W最小,最小值为2500元.
故购买A种树苗50棵、B种树苗50棵时所付的种植工钱最少,最少工钱是2500元.
【解析】(1)设购买A种树苗每棵需要x元,B种树苗每棵需要y元,根据总价=单价×数量,可列出关于x、y的二元一次方程组,解方程组即可得出结论;(2)设购买A种树苗m棵,则购买B种树苗100﹣m棵,根据总价=单价×数量,可列出关于m的一元一次不等式组,解不等式组即可得出m的取值范围,由此可得出结论;(3)设种植工钱为W,根据植树的工钱=植A种树的工钱+植乙种数的工钱,列出W关于m的函数关系式,根据一次函数的单调性即可解决最值问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校需要招聘一名教师,对三名应聘者进行了三项素质测试
 下面是三名应聘者的综合测试成绩:
下面是三名应聘者的综合测试成绩:应聘者
成绩
项目
A
B
C
基本素质
70
65
75
专业知识
65
55
50
教学能力
80
85
85
(1)如果根据三项测试的平均成绩确定录用教师,那么谁将被录用?
(2)学校根据需要,对基本素质、专业知识、教学能力的要求不同,决定按2:1:3的比例确定其重要性,那么哪一位会被录用?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在求1+3+32+33+34+35+36+37+38的值时,李敏发现:从第二个加数起每一个加数都是前一个加数的3倍,于是她假设:S=1+3+32+33+34+35+36+37+38①,
然后在①式的两边都乘3,得3S=3+32+33+34+35+36+37+38+39②
②-①得,3S-S=39-1,即2S=39-1,
所以S=
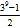 .
.得出答案后,爱动脑筋的张红想:如果把“3”换成字母a(a≠0且a≠1),能否求出1+a+a2+a3+a4+…+a2 017的值?如能求出,其正确答案是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线AB,CD相交于点O,OE平分∠AOD,FO⊥AB,垂足为O,
 ∠BOD=∠DOE.
∠BOD=∠DOE.(1)求∠BOF的度数;
(2)请写出图中与∠BOD相等的所有的角.

-
科目: 来源: 题型:
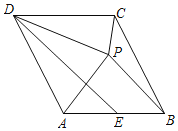
查看答案和解析>>【题目】在菱形ABCD中,
 ,点E为AB边的中点,点P与点A关于DE对称,连接DP、BP、CP,下列结论:
,点E为AB边的中点,点P与点A关于DE对称,连接DP、BP、CP,下列结论: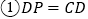 ;
;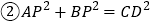 ;
;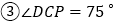 ;
;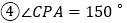 ,其中正确的是
,其中正确的是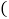
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料: 如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2=
 交于A(1,3)和B(﹣3,﹣1)两点.
交于A(1,3)和B(﹣3,﹣1)两点.
观察图象可知:
①当x=﹣3或1时,y1=y2;
②当﹣3<x<0或x>1时,y1>y2 , 即通过观察函数的图象,可以得到不等式ax+b> 的解集.
的解集.
有这样一个问题:求不等式x3+4x2﹣x﹣4>0的解集.
某同学根据学习以上知识的经验,对求不等式x3+4x2﹣x﹣4>0的解集进行了探究.
下面是他的探究过程,请将探究过程补充完整:
将不等式按条件进行转化:
当x=0时,原不等式不成立;
当x>0时,原不等式可以转化为x2+4x﹣1> ;
;
当x<0时,原不等式可以转化为x2+4x﹣1< ;
;
(1)构造函数,画出图象 设y3=x2+4x﹣1,y4= ,在同一坐标系中分别画出这两个函数的图象.
,在同一坐标系中分别画出这两个函数的图象.
双曲线y4= 如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
(2)确定两个函数图象公共点的横坐标 观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为;
(3)借助图象,写出解集 结合(1)的讨论结果,观察两个函数的图象可知:不等式x3+4x2﹣x﹣4>0的解集为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】探究题
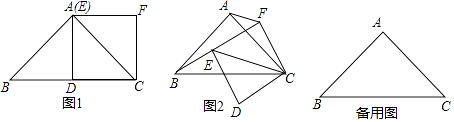
(1)【问题发现】
如图1,在Rt△ABC中,AB=AC=2,∠BAC=90°,点D为BC的中点,以CD为一边作正方形CDEF,点E恰好与点A重合,则线段BE与AF的数量关系为
(2)【拓展研究】
在(1)的条件下,如果正方形CDEF绕点C旋转,连接BE,CE,AF,线段BE与AF的数量关系有无变化?请仅就图2的情形给出证明;
(3)【问题发现】
当正方形CDEF旋转到B,E,F三点共线时候,直接写出线段AF的长.
相关试题

