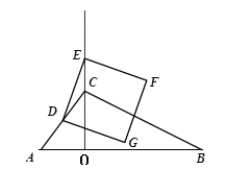
【题目】如图,已知△ABC,CO⊥AB于O,且CO=8,AB=22,sinA=![]() ,点D为AC的中点,点E为射线OC上任意一点,连结DE,以DE为边在DE的右侧按顺时针方向作正方形DEFG,设OE=x.
,点D为AC的中点,点E为射线OC上任意一点,连结DE,以DE为边在DE的右侧按顺时针方向作正方形DEFG,设OE=x.
(1)求AD的长;
(2)记正方形DEFG的面积为y,① 求y关于x的函数关系式;② 当DF∥AB时,求y的值;
(3)是否存在x的值,使正方形的顶点F或G落在△ABC的边上?若存在,求出所有满足条件的x的值;若不存在,说明理由。
参考答案:
【答案】(1)5;(2)y=(x-4)2+9;18;(3)![]() 或21或3或
或21或3或![]() .
.
【解析】(2)①如图1,过点D作DE⊥y轴于H,则EH=|n-4|,根据正方形的面积公式和勾股定理可得S关于n的函数关系式;
②当DF∥x轴时,点H即为正方形DEFG的中心,可得n=7,再代入函数关系式即可得到S的值;
(3)根据待定系数法可得BC为:y=![]() x+8,再分四种情况:①当点F落在BC上时;②当点G落在BC上时;③当点F落在AB上时;④当点G落在AB上时;
x+8,再分四种情况:①当点F落在BC上时;②当点G落在BC上时;③当点F落在AB上时;④当点G落在AB上时;
矩形讨论可得所有满足条件的n的值.
(1)AD=5
(2)①如图所示,过点D作DH⊥OC于H,

∴y=DE2= EH2 +DH2=(x-4)2+9
②当DF∥AB时,点H即为正方形DEFG的中心
∴EH=DH=3
∴x=4+3=7
∴y=(7-4)2+9=18
(3)①当点F落在BC边上时,如图所示,

由△DEM≌△EFN
得x=![]()
②当点G落在BC边上时,如图所示,
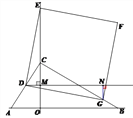
由△DEM≌△GDN
得x=21
③当点F落在AB边上时,如图所示,

由①同理可得△DEM≌△EFO
即x=3
④当点G落在AC边上时,如图所示,
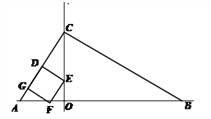
由△DCE∽△OCA
得x=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的三条线段能组成三角形的是( )
A.5cm 2cm 3cm
B.5cm 2cm 2cm
C.5cm 2cm 4cm
D.5cm 12cm 6cm -
科目: 来源: 题型:
查看答案和解析>>【题目】探索规律
观察下列各式及验证过程:n=2时,有式①: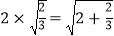 ;n=3时,有式②:
;n=3时,有式②: 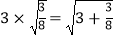 ;
;
式①验证: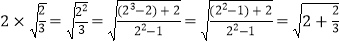
式②验证: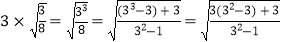
(1)针对上述式①、式②的规律,请写出n=4时的式子;
(2)请写出满足上述规律的用n(n为任意自然数,且n≥2)表示的等式,并加以验证. -
科目: 来源: 题型:
查看答案和解析>>【题目】一只不透明的袋子中装有1个白球、2个黄球和3个红球,每个球除颜色外都相同,将球摇匀,从中任意摸出一个球:
(1)该球是白球;
(2)该球是黄球;
(3)该球是红球.
估计上述事件发生的可能性的大小,将这些事件的序号按发生的可能性从小到大的顺序排列. -
科目: 来源: 题型:
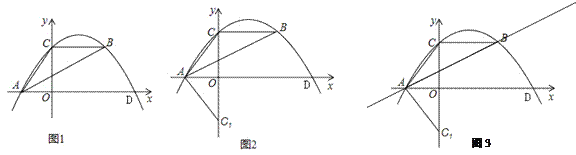
查看答案和解析>>【题目】如图1,抛物线y=ax2﹣10ax+c经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,OA=
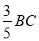 且AC=BC.
且AC=BC.(1)求抛物线的解析式;
(2)如图2,将△AOC沿x轴对折得到△AOC1,再将△AOC1绕平面内某点旋转180°后得△A1O1C2(A,O,C1分别与点A1,O1,C2对应)使点A1,C2在抛物线上,求A1,C2的坐标.
(3)如图3,若Q为直线AB上一点,直接写出|QC﹣QD|的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:8(x4)6-2(x5·x3)3+(-3x6)3·x4·x2+x3÷x;
(2)若ax=3,b2x=2,求(a2)x-(b3x)2的值.
相关试题

