搜索
【题目】(1)计算：8(x4)6－2(x5·x3)3＋(－3x6)3·x4·x2＋x3÷x；
(2)若ax＝3，b2x＝2，求(a2)x－(b3x)2的值．
参考答案：
【答案】（1）－21x24＋x2.（2）1.
【解析】
（1）根据幂的混合运算法则计算即可；
（2）利用幂的乘方法则把 (a2)x－(b3x)2变形为(ax)2－(b2x)3即可得到结论．
（1）原式=8x24－2(x8)3－27x18·x6＋x2=8x24－2x24－27x24＋x2=－21x24＋x2．
（2）原式=a2x－b6x =(ax)2－(b2x)3=9－8=1．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC,CO⊥AB于O,且CO=8，AB=22，sinA=
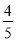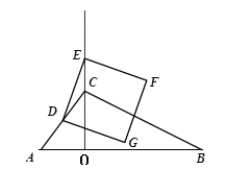
,点D为AC的中点，点E为射线OC上任意一点，连结DE，以DE为边在DE的右侧按顺时针方向作正方形DEFG，设OE=x．（1）求AD的长；
（2）记正方形DEFG的面积为y，① 求y关于x的函数关系式；② 当DF∥AB时，求y的值；
（3）是否存在x的值，使正方形的顶点F或G落在△ABC的边上？若存在，求出所有满足条件的x的值；若不存在，说明理由。
-
科目： 来源： 题型：
查看答案和解析>>【题目】一只不透明的袋子中装有1个白球、2个黄球和3个红球，每个球除颜色外都相同，将球摇匀，从中任意摸出一个球：
（1）该球是白球；
（2）该球是黄球；
（3）该球是红球．
估计上述事件发生的可能性的大小，将这些事件的序号按发生的可能性从小到大的顺序排列． -
科目： 来源： 题型：
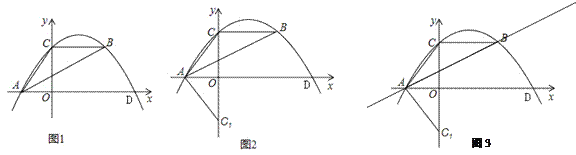
查看答案和解析>>【题目】如图1，抛物线y=ax2﹣10ax+c经过△ABC的三个顶点，已知BC∥x轴，点A在x轴上，点C在y轴上，OA=
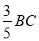且AC=BC．（1）求抛物线的解析式；
（2）如图2，将△AOC沿x轴对折得到△AOC1，再将△AOC1绕平面内某点旋转180°后得△A1O1C2（A，O，C1分别与点A1，O1，C2对应）使点A1，C2在抛物线上，求A1，C2的坐标．
（3）如图3，若Q为直线AB上一点，直接写出|QC﹣QD|的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一元二次方程x(x+4)=8x+12的一般形式是_______________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在一个不透明的袋子中装有1个白球，2个黄球和3个红球，每个除颜色外完全相同，将球摇匀从中任取一球：（1）恰好取出白球；
（2）恰好取出红球；
（3）恰好取出黄球，
根据你的判断，将这些事件按发生的可能性从小到大的顺序排列 （只需填写序号）． -
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两位同学在一次用频率估计概率的实验中统计了某一结果出现的频率给出的统计图如图所示，则符合这一结果的实验可能是（ ）
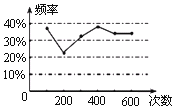
A.掷一枚正六面体的骰子，出现5点的概率
B.掷一枚硬币，出现正面朝上的概率
C.任意写出一个整数，能被2整除的概率
D.一个袋子中装着只有颜色不同，其他都相同的两个红球和一个黄球，从中任意取出一个是黄球的概率
相关试题
