【题目】已知二次函数y=ax2+bx+c的图象经过点A(1,0).
(1)当b=2,c=﹣3时,求二次函数的解析式及二次函数最小值;
(2)二次函数的图象经过点B(m,e),C(3﹣m,e). ①求该二次函数图象的对称轴;
②若对任意实数x,函数值y都不小于 ![]() ﹣
﹣ ![]() ,求此时二次函数的解析式.
,求此时二次函数的解析式.
参考答案:
【答案】
(1)解:将b=2,c=﹣3代入得:y=ax2+2x﹣3.
将x=1,y=0代入,a+2﹣3=0,
∴a=1.
∴y=x2+2x﹣3=(x+1)2﹣4,
∴当x=﹣1时,y最小值为﹣4.
(2)解:①由题意可知:对称轴x= ![]() =
= ![]() .
.
②∵﹣ ![]() =
= ![]() ,
,
∴b=﹣3a,又∵a+b+c=0,
∴c=2a,
∴y=ax2﹣3ax+2a
顶点纵坐标为 ![]() =
= ![]() ,
,
∵函数值不小于 ![]() ﹣
﹣ ![]() ,
,
∴a>0,且﹣ ![]() ≥
≥ ![]() ﹣
﹣ ![]() ,
,
∴a2﹣2a+1≤0,
∴(a﹣1)2≤0,
∵(a﹣1)2≥0,
∴a﹣1=0,
∴a=1.
【解析】(1)利用待定系数法以及配方法即可解决问题.(2)①根据对称性B、C关于对称轴对称,即可解决问题.②首先求出b、c(用a表示),想办法列出不等式即可解决问题.
【考点精析】通过灵活运用二次函数的性质,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段MN=3cm,在线段MN上取一点P,使PM=PN;延长线段MN到点A,使AN=
 MN;延长线段NM到点B,使BN=3BM.
MN;延长线段NM到点B,使BN=3BM.(1)根据题意,画出图形;
(2)求线段AB的长;
(3)试说明点P是哪些线段的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请根据下面X与Y的对话解答下列各小题:
X:我和Y都是多边形,我们俩的内角和相加的结果为1440°;
Y:X的边数与我的边数之比为1∶3.
(1)求X与Y的外角和相加的度数;
(2)分别求出X与Y的边数;
(3)试求出Y共有多少条对角线?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:AB,PQ是圆O的两条直径,连接PB,AQ.
(1)如图①,求证:AQ∥BP,AG∥BP;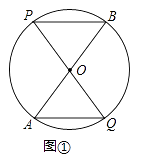
(2)如图②,过点B作BC⊥PQ于点D,交圆O于点C,在DG上取一点K,使DK=DP,求证:四边形AQKC是平行四边形.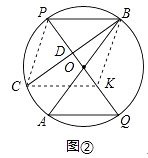
-
科目: 来源: 题型:
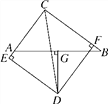
查看答案和解析>>【题目】如图,在△ABC中,AC=6,BC=8,∠BCA的平分线与AB边的垂直平分线相交于点D,DE⊥AC,DF⊥BC,垂足分别是E、F.
(1)求证:AE=BF;
(2)求AE的长.
-
科目: 来源: 题型:
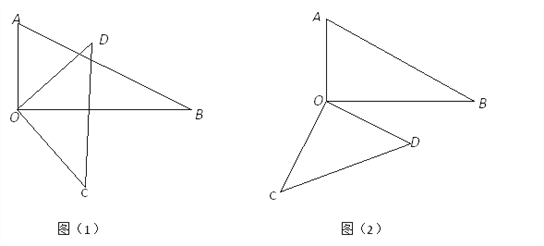
查看答案和解析>>【题目】将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起.
(1)如图(1)若∠BOD=35°,求∠AOC的度数,若∠AOC=135°,求∠BOD的度数。
(2)如图(2)若∠AOC=150°,求∠BOD的度数
(3)猜想∠AOC与∠BOD的数量关系,并结合图(1)说明理由.
(4)三角尺AOB不动,将三角尺COD的OD边与OA边重合,然后绕点O按顺时针或逆时针方向任意转动一个角度,当∠AOD(0°<∠AOD<90°)等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠AOD角度所有可能的值,不用说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为4的顶点开始,第2018次“移位”后,那么他所处的顶点的编号是( )

A. 1 B. 2 C. 3 D. 4
相关试题

