【题目】已知:AB,PQ是圆O的两条直径,连接PB,AQ.
(1)如图①,求证:AQ∥BP,AG∥BP; 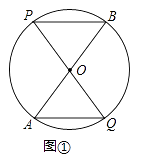
(2)如图②,过点B作BC⊥PQ于点D,交圆O于点C,在DG上取一点K,使DK=DP,求证:四边形AQKC是平行四边形. 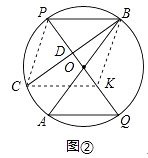
参考答案:
【答案】
(1)证明:∵ ![]() =
= ![]() ,
,
∴∠P=∠A,
∵OA=OQ,
∴∠A=∠Q,
∴∠P=∠Q,
∴AQ∥PB.
∵∠AOQ=∠BOP,
∴ ![]() =
= ![]() ,
,
∴AQ=BP;
(2)证明:∵PQ⊥BC,
∴BD=CD,
又∵PD=DK,
∴BC与PK互相垂直且平分,
∴四边形BKCP为菱形;
∴PB∥CK,且PB=CK,
∵PB∥AQ,
∴CK∥AQ,
∵PB=AQ,
∴CK=AQ,
∵CK∥AQ,且CK=AQ,
∴四边形AQKC为平行四边形.
【解析】(1)由同弧所对的圆周角相等得出∠P=∠A,由OA=OQ得出∠A=∠Q,那么∠P=∠Q,AQ∥PB.根据∠AOQ=∠BOP,得到 ![]() =
= ![]() ,那么AQ=BP;(2)先由垂径定理得出BD=CD,又PD=DK,得出四边形BKCP为菱形,根据菱形的性质得出PB∥CK,再证明CK∥AQ,且CK=AQ,那么四边形AQKC为平行四边形.
,那么AQ=BP;(2)先由垂径定理得出BD=CD,又PD=DK,得出四边形BKCP为菱形,根据菱形的性质得出PB∥CK,再证明CK∥AQ,且CK=AQ,那么四边形AQKC为平行四边形.
【考点精析】本题主要考查了平行四边形的判定和圆周角定理的相关知识点,需要掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在半径为50的⊙O中,弦AB的长为50,
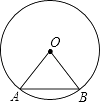
(1)求∠AOB的度数;
(2)求点O到AB的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段MN=3cm,在线段MN上取一点P,使PM=PN;延长线段MN到点A,使AN=
 MN;延长线段NM到点B,使BN=3BM.
MN;延长线段NM到点B,使BN=3BM.(1)根据题意,画出图形;
(2)求线段AB的长;
(3)试说明点P是哪些线段的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请根据下面X与Y的对话解答下列各小题:
X:我和Y都是多边形,我们俩的内角和相加的结果为1440°;
Y:X的边数与我的边数之比为1∶3.
(1)求X与Y的外角和相加的度数;
(2)分别求出X与Y的边数;
(3)试求出Y共有多少条对角线?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象经过点A(1,0).
(1)当b=2,c=﹣3时,求二次函数的解析式及二次函数最小值;
(2)二次函数的图象经过点B(m,e),C(3﹣m,e). ①求该二次函数图象的对称轴;
②若对任意实数x,函数值y都不小于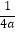 ﹣
﹣  ,求此时二次函数的解析式.
,求此时二次函数的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=6,BC=8,∠BCA的平分线与AB边的垂直平分线相交于点D,DE⊥AC,DF⊥BC,垂足分别是E、F.
(1)求证:AE=BF;
(2)求AE的长.
-
科目: 来源: 题型:
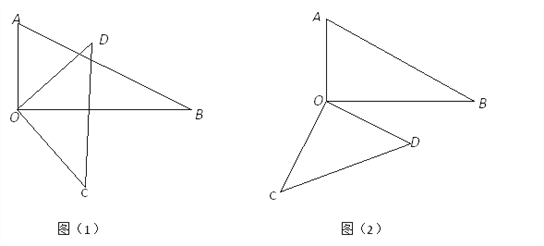
查看答案和解析>>【题目】将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起.
(1)如图(1)若∠BOD=35°,求∠AOC的度数,若∠AOC=135°,求∠BOD的度数。
(2)如图(2)若∠AOC=150°,求∠BOD的度数
(3)猜想∠AOC与∠BOD的数量关系,并结合图(1)说明理由.
(4)三角尺AOB不动,将三角尺COD的OD边与OA边重合,然后绕点O按顺时针或逆时针方向任意转动一个角度,当∠AOD(0°<∠AOD<90°)等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠AOD角度所有可能的值,不用说明理由.
相关试题

