【题目】如图,在平面直角坐标系中,△ABC内接于⊙P,AB是⊙P的直径,A(﹣1,0)C(3,2 ![]() ),BC的延长线交y轴于点D,点F是y轴上的一动点,连接FC并延长交x轴于点E.
),BC的延长线交y轴于点D,点F是y轴上的一动点,连接FC并延长交x轴于点E. 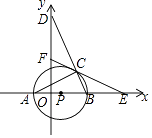
(1)求⊙P的半径;
(2)当∠A=∠DCF时,求证:CE是⊙P的切线.
参考答案:
【答案】
(1)解:作CG⊥x轴于G,
则AC2=AG2+CG2=(3+1)2+(2 ![]() )2=24,
)2=24,
由射影定理得:AC2=AGAB,
∴AB= ![]() =6,
=6,
∴⊙P的半径为3
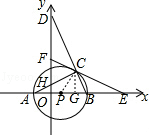
(2)解:证明:连接PC,
∵AB是⊙P的直径,
∴∠ACB=90°,
∴∠CAB+∠CBA=90°,
∵PC=PB,
∴∠PCB=∠PBC,
∵∠A=∠DCF=∠ECB,
∴∠ECB+∠PCB=90°,
∵C在⊙P上,
∴CE是⊙P的切线.
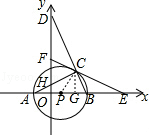
【解析】(1)作CG⊥x轴于G,根据勾股定理和射影定理即可得到结论;(2)连接PC,由AB是⊙P的直径,得到∠ACB=90°根据等腰三角形的性质得到∠PCB=∠PBC,根据切线的判定定理即可得到结论.
【考点精析】通过灵活运用三角形的外接圆与外心和切线的判定定理,掌握过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)是一个晾衣架的实物图,支架的基本图形是菱形,MN是晾衣架的一个滑槽,点P在滑槽MN上、下移动时,晾衣架可以伸缩,其示意图如图(2)所示,已知每个菱形的边长均为20cm,且AB=CD=CP=DM=20cm.
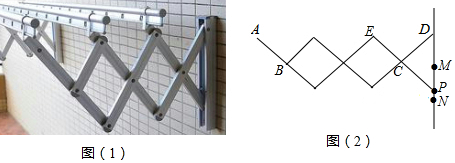
(1)当点P向下滑至点N处时,测得∠DCE=60°时 ①求滑槽MN的长度;
②此时点A到直线DP的距离是多少?
(2)当点P向上滑至点M处时,点A在相对于(1)的情况下向左移动的距离是多少? (结果精确到0.01cm,参考数据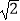 ≈1.414,
≈1.414, 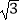 ≈1.732)
≈1.732) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )

A. 2 B. 3 C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC的面积为84,BC=21,现将△ABC沿直线BC向右平移a(0<a<21)个单位到△DEF的位置.
(1)求BC边上的高;
(2)若AB=10,
①求线段DF的长;
②连结AE,当△ABE时等腰三角形时,求a的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(﹣2,﹣4),直线x=﹣2与x轴相交于点B,连接OA,抛物线y=﹣x2从点O沿OA方向平移,与直线x=﹣2交于点P,顶点M到点A时停止移动.
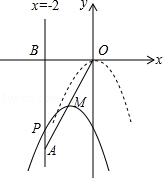
(1)线段OA所在直线的函数解析式是;
(2)设平移后抛物线的顶点M的横坐标为m,问:当m为何值时,线段PA最长?并求出此时PA的长.
(3)若平移后抛物线交y轴于点Q,是否存在点Q使得△OMQ为等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,我们把横 、纵坐标都是整数的点叫做整点.已知点
中,我们把横 、纵坐标都是整数的点叫做整点.已知点A(0,4),点B是
 轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ▲ ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)
轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ▲ ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解
如图(1),在正多边形A1A2A3…An的边A2A3上任取一不与点A2重合的点B2 , 并以线段A1B2为边在线段A1A2的上方作以正多边形A1B2B3…Bn , 把正多边形A1B2B3…Bn叫正多边形A1A2…An的准位似图形,点A3称为准位似中心.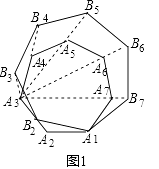
特例论证
(1)如图(2)已知正三角形A1A2A3的准位似图形为正三角形A1B2B3 , 试证明:随着点B2的运动,∠B3A3A1的大小始终不变.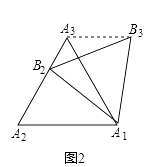
(2)如图(3)已知正方形A1A2A3A4的准位似图形为正方形A1B2B3B4 , 随着点B2的运动,∠B3A3A4的大小始终不变?若不变,请求出∠B3A3A4的大小;若改变,请说明理由.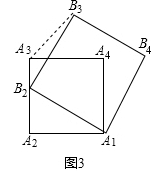
(3)在图(1)的情况下:
①试猜想∠B3A3A4的大小是否会发生改变?若不改变,请用含n的代数式表示出∠B3A3A4的大小(直接写出结果);若改变,请说明理由.
①∠B3A3A4+∠B4A4A5+∠B5A5A6+…+∠BnAnA1= (用含n的代数式表示)
(用含n的代数式表示)
相关试题

