【题目】如图,在平面直角坐标系中,已知点A(﹣2,﹣4),直线x=﹣2与x轴相交于点B,连接OA,抛物线y=﹣x2从点O沿OA方向平移,与直线x=﹣2交于点P,顶点M到点A时停止移动.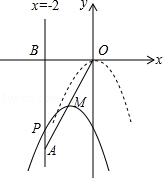
(1)线段OA所在直线的函数解析式是;
(2)设平移后抛物线的顶点M的横坐标为m,问:当m为何值时,线段PA最长?并求出此时PA的长.
(3)若平移后抛物线交y轴于点Q,是否存在点Q使得△OMQ为等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)y=2x
(2)
解:设M点的坐标为(m,2m),(﹣2≤m<0),
∴平移后抛物线解析式为y=﹣(x﹣m)2+2m,
当x=﹣2时,y=﹣(2﹣m)2+2m=﹣m2﹣2m﹣4,
∴P点的坐标为(﹣2,﹣m2﹣2m﹣4),
∴PA=﹣m2﹣2m﹣4﹣(﹣4)=﹣m2﹣2m=﹣(m﹣1)2+1
∴当m=1时,PA的值最大,PA的最大值为1
(3)
解:存在,理由如下:
当x=0时,y=﹣(0﹣m)2+2m=﹣m2+2m,则Q(0,﹣m2+2m),
∵OQ=m2﹣2m,OM= ![]() =﹣
=﹣ ![]() m,
m,
当OM=OQ,即﹣ ![]() m=m2﹣2m,即m2﹣(2﹣
m=m2﹣2m,即m2﹣(2﹣ ![]() )m=0,解得m1=0(舍去),m2=2﹣
)m=0,解得m1=0(舍去),m2=2﹣ ![]() ,此时Q点坐标为(0,5﹣2
,此时Q点坐标为(0,5﹣2 ![]() );
);
当OM=MQ,作MH⊥OQ于H,如图1,则OH=QH,﹣2m=m2﹣2m﹣(﹣2m),
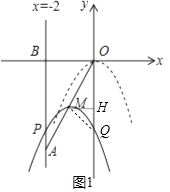
即m2+2m=0,解得m1=0(舍去),m2=﹣2,此时Q点坐标为(0,﹣8);
当QM=QO,作QF⊥OM于F,如图2,则OF=MF=﹣ ![]() m,
m,

∵OQ∥AB,
∴∠QOF=∠BAO,
∴Rt△OFQ∽Rt△ABO,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,整理得4m2﹣3m=0,解得m1=0(舍去),m2=
,整理得4m2﹣3m=0,解得m1=0(舍去),m2= ![]() (舍去),
(舍去),
综上所述,满足条件的Q点坐标为(0,5﹣2 ![]() )或(0,﹣8).
)或(0,﹣8).
【解析】解:(1)设直线OA的解析式为y=kx,
把(﹣2,﹣4)代入得﹣2k=﹣4,解得k=2,
所以直线OA的解析式为y=2x;
所以答案是y=2x;
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )

A. 2 B. 3 C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC的面积为84,BC=21,现将△ABC沿直线BC向右平移a(0<a<21)个单位到△DEF的位置.
(1)求BC边上的高;
(2)若AB=10,
①求线段DF的长;
②连结AE,当△ABE时等腰三角形时,求a的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC内接于⊙P,AB是⊙P的直径,A(﹣1,0)C(3,2
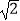 ),BC的延长线交y轴于点D,点F是y轴上的一动点,连接FC并延长交x轴于点E.
),BC的延长线交y轴于点D,点F是y轴上的一动点,连接FC并延长交x轴于点E. 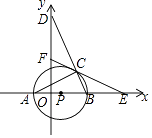
(1)求⊙P的半径;
(2)当∠A=∠DCF时,求证:CE是⊙P的切线. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,我们把横 、纵坐标都是整数的点叫做整点.已知点
中,我们把横 、纵坐标都是整数的点叫做整点.已知点A(0,4),点B是
 轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ▲ ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)
轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ▲ ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解
如图(1),在正多边形A1A2A3…An的边A2A3上任取一不与点A2重合的点B2 , 并以线段A1B2为边在线段A1A2的上方作以正多边形A1B2B3…Bn , 把正多边形A1B2B3…Bn叫正多边形A1A2…An的准位似图形,点A3称为准位似中心.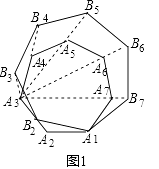
特例论证
(1)如图(2)已知正三角形A1A2A3的准位似图形为正三角形A1B2B3 , 试证明:随着点B2的运动,∠B3A3A1的大小始终不变.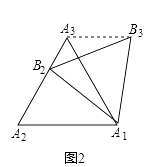
(2)如图(3)已知正方形A1A2A3A4的准位似图形为正方形A1B2B3B4 , 随着点B2的运动,∠B3A3A4的大小始终不变?若不变,请求出∠B3A3A4的大小;若改变,请说明理由.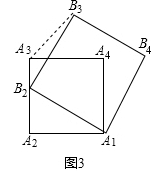
(3)在图(1)的情况下:
①试猜想∠B3A3A4的大小是否会发生改变?若不改变,请用含n的代数式表示出∠B3A3A4的大小(直接写出结果);若改变,请说明理由.
①∠B3A3A4+∠B4A4A5+∠B5A5A6+…+∠BnAnA1= (用含n的代数式表示)
(用含n的代数式表示) -
科目: 来源: 题型:
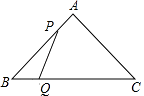
查看答案和解析>>【题目】如图,△ABC中,AB=AC=10,BC=12,动点P从A点出发,按A→B的方向在AB上移动,动点Q从B点出发,按B→C的方向在BC上移动(当P点到达点B时,P点和Q点停止移动,且两点的移动速度相等),记PA=x,△BPQ的面积为y,则y关于x的函数图象大致是( )
A.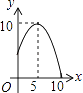
B.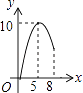
C.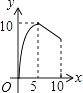
D.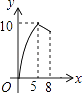
相关试题

