Question

【题目】如图，在平面直角坐标系中，直线y= x﹣1与抛物线y=﹣ x2+bx+c交于A，B两点，点A在x轴上，点B的横坐标为﹣8，点P是直线AB上方的抛物线上的一动点（不与点A，B重合）．

（1）求该抛物线的函数关系式；
（2）连接PA、PB，在点P运动过程中，是否存在某一位置，使△PAB恰好是一个以点P为直角顶点的等腰直角三角形，若存在，求出点P的坐标；若不存在，请说明理由；
（3）过P作PD∥y轴交直线AB于点D，以PD为直径作⊙E，求⊙E在直线AB上截得的线段的最大长度．

Answer 1

【答案】
（1）

解：∵点A在x轴上，点B的横坐标为﹣8，且在直线y= x﹣1，

∴A（2，0），B（﹣8，﹣5），

∵点A，B在抛物线y=﹣ x2+bx+c上，

∴0=﹣1+2b+c，﹣16﹣8b+c=﹣5，

∴b=﹣1，c=3，

∴抛物线的解析式为y=﹣ x2﹣x+3

（2）

解：假设存在这样点P，使△PAB恰好是一个直角三角形，

∵△PAB恰好是一个直角三角形，直线y= x﹣1与抛物线y=﹣ x 2+bx+c交于A、B两点，P为抛物线上的点，

∴只能是∠APB=90°，即AP⊥PB，

∴直线AP和直线PB的斜率乘积等于﹣1，

设P（x，﹣ x 2﹣x+3），而A坐标为（2，0），B坐标为（﹣8，﹣5），

∴ × =﹣1，

∴（x+6）（x﹣4）=﹣16，

解得x=2（舍）或x=﹣4．

∴P（﹣4，3），

∵A（2，0），B（﹣8，﹣5），

∴PA= =3 ，PB= =4 ，

∴PA≠PB，

∴不存在使△PAB恰好是一个以点P为直角顶点的等腰直角三角形

（3）

解：如图，

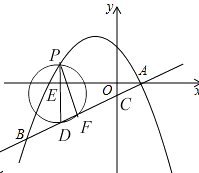
∵OA=2，OC=1，

∴AC= ，

∵PD∥OC，

∴∠OCA=∠QDF，

∵∠PFD=∠AOC=90°，

∴△AOC∽△PFD，

∴ = = ，

∴DF= PD，

设D（x， x﹣1），P（x，﹣ x2﹣x+3），

∴PD=﹣ x2﹣x+3﹣ x+1=﹣ x2﹣ x+4，

∴DF=PD= ×（﹣ x2﹣ x+4），

∴当x=﹣3时，DF最大= ×（﹣ ×32+ ×3+4）=

【解析】（1）根据直线y= x﹣1与抛物线y=﹣ x2+bx+c交于A、B两点，点A在x轴上，点B的横坐标为﹣8，求出点A（2，0），B（﹣8，﹣5）利用待定系数法求出抛物线解析式；（2）假设存在这样点P，使△PAB恰好是一个直角三角形，只有∠APB=90°，即AP⊥PB，设出点P的坐标，表示出直线PA，PB的解析式，由直线AP和直线PB的斜率乘积等于﹣1建立方程，则可求得点P的坐标，再利用勾股定理求得PA和PB，进行判断即可；（3）先判断出∠OCA=∠QDF进而得出△AOC∽△PFD，得出DF= PD，最后建立DF=PD= ×（﹣ x2﹣ x+4），即可得出结论．