搜索
【题目】如图，△ABC的边AC与⊙O相交于C，D两点，且经过圆心O，边AB与⊙O相切，切点为B．如果∠A=34°，那么∠C等于（ ） 
A.28°
B.33°
C.34°
D.56°
参考答案：
【答案】A
【解析】解：连结OB，如图，
∵AB与⊙O相切，
∴OB⊥AB，
∴∠ABO=90°，
∴∠AOB=90°﹣∠A=90°﹣34°=56°，
∵∠AOB=∠C+∠OBC，
∴∠C+∠OBC=56°，
而OB=OC，
∴∠C=∠OBC，
∴∠C= 
×56°=28°．
故选A．
连结OB，如图，根据切线的性质得∠ABO=90°，则利用互余可计算出∠AOB=90°﹣∠A=56°，再利用三角形外角性质得∠C+∠OBC=56°，加上∠C=∠OBC，于是有∠C= ×56°=28°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，射线AM上有一点B，AB=6，点C是射线AM上异于B的一点，过C作CD⊥AM，且CD=
AC，过D点作DE⊥AD，交射线AM于E，在射线CD取点F，使得CF=CB，连接AF并延长，交DE于点G，设AC=3x．
（1）当C在B点右侧时，求AD．DF的长．（用关于x的代数式表示）
（2）当x为何值时，△AFD是等腰三角形；
（3）作点D关于AG的对称点D′，连接FD′，GD′，若四边形DFD′G是平行四边形，求x的值．（直接写出答案） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，直线y=
x﹣1与抛物线y=﹣ 
x2+bx+c交于A，B两点，点A在x轴上，点B的横坐标为﹣8，点P是直线AB上方的抛物线上的一动点（不与点A，B重合）．
（1）求该抛物线的函数关系式；
（2）连接PA、PB，在点P运动过程中，是否存在某一位置，使△PAB恰好是一个以点P为直角顶点的等腰直角三角形，若存在，求出点P的坐标；若不存在，请说明理由；
（3）过P作PD∥y轴交直线AB于点D，以PD为直径作⊙E，求⊙E在直线AB上截得的线段的最大长度． -
科目： 来源： 题型：
查看答案和解析>>【题目】某中学初三（1）班共有40名同学，在一次30秒跳绳测试中他们的成绩统计如下表：
跳绳数/个
81
85
90
93
95
98
100
人 数
1
2
8
11
5
将这些数据按组距5（个）分组，绘制成如图的频数分布直方图（不完整）．
（1）将表中空缺的数据填写完整，并补全频数分布直方图；
（2）这个班同学这次跳绳成绩的众数是个，中位数是个；
（3）若跳满90个可得满分，学校初三年级共有720人，试估计该中学初三年级还有多少人跳绳不能得满分．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，抛物线y=ax2+bx+c（a，b，c是常数，a＞0）的部分图象如图所示，直线x=1是它的对称轴．若一元二次方程ax2+bx+c=0的一个根x1的取值范围是2＜x1＜3，则它的另一个根x2的取值范围是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】把大小完全相同的6个乒乓球分成两组，每组3个，每组乒乓球上面分别标有数字1，2，3，将这两组乒乓球分别放入两个盒子中搅匀，再从每个盒子中各随机取出1个乒乓球，请用画树状图（或列表）的方法，求取出的2个乒乓球上面数字之和为偶数的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某市开展一项自行车旅游活动，线路需经A、B、C、D四地，如图，其中A、B、C三地在同一直线上，D地在A地北偏东30°方向，在C地北偏西45°方向，C地在A地北偏东75°方向．且BC=CD=20km，问沿上述线路从A地到D地的路程大约是多少？（最后结果保留整数，参考数据：sin15°≈0.25，cos15°≈0.97，tan15°≈0.27，
）
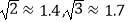相关试题
