Question

【题目】某中学初三（1）班共有40名同学，在一次30秒跳绳测试中他们的成绩统计如下表：

跳绳数/个	81	85	90	93	95	98	100
人 数	1	2		8	11		5

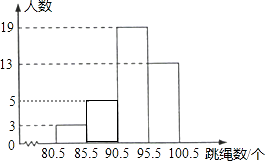
将这些数据按组距5（个）分组，绘制成如图的频数分布直方图（不完整）．
（1）将表中空缺的数据填写完整，并补全频数分布直方图；
（2）这个班同学这次跳绳成绩的众数是个，中位数是个；
（3）若跳满90个可得满分，学校初三年级共有720人，试估计该中学初三年级还有多少人跳绳不能得满分．

Answer 1

【答案】
（1）解：根据直方图得到95.5﹣100.5小组共有13人，由统计表知道跳100个的有5人，

∴跳98个的有13﹣5=8人，

跳90个的有40﹣1﹣2﹣8﹣11﹣8﹣5=5人，

故统计表为：

跳绳数/个	81	85	90	93	95	98	100
人 数	1	2	5	8	11	8	5

直方图为：

（2）95；95
（3）解：估计该中学初三年级不能得满分的有720× =54人
【解析】解：（2）观察统计表知：众数为95个，中位数为95个； （1）首先根据直方图得到95.5﹣100.5小组共有13人，由统计表知道跳100个的有5人，从而求得跳98个的人数；（2）根据众数和中位数的定义填空即可；（3）用样本估计总体即可．