【题目】已知:用3辆A型车和2辆B型车载满货物一次可运货共19吨;用2辆A型车和3辆B型车载满货物一次可运货共21吨.
(1)1辆A型车和1辆B型车都载满货物一次分别可以运货多少吨?
(2)某物流公司现有49吨货物,计划同时租用A型车![]() 辆,B型车
辆,B型车![]() 辆,一次运完,且恰好每辆车都载满货物.
辆,一次运完,且恰好每辆车都载满货物.
①求![]() 、
、![]() 的值;
的值;
②若A型车每辆需租金130元/次,B型车每辆需租金200元/次.请求出租车费用最少是多少元?
参考答案:
【答案】(1)1辆A型车一次可以运货3吨,1辆B型车一次可以运货5吨;(2)①![]() 或
或 ![]() 或
或 ![]() ,②租车费用最少的是1990元
,②租车费用最少的是1990元
【解析】分析:(1)设1辆A型车和1辆B型车都载满货物一次分别可以运货![]() 吨,
吨,![]() 吨,根据题意列二元一次方程组求解;(2)①结合(1)中的数据,列二元一次方程,根据m,n的实际意义求解;②分别求出每一种运输方案的费用,再作比较.
吨,根据题意列二元一次方程组求解;(2)①结合(1)中的数据,列二元一次方程,根据m,n的实际意义求解;②分别求出每一种运输方案的费用,再作比较.
详解:(1)设1辆A型车和1辆B型车都载满货物一次分别可以运货![]() 吨,
吨,![]() 吨,
吨,
根据题意得:![]() ,
,
解得:![]() .
.
答:1辆A型车一次可以运货3吨,1辆B型车一次可以运货5吨.
(2)①由(1)和题意得:![]() ,
,
∴![]() .
.
∵![]() ,
,![]() 都是正整数,
都是正整数,
∴![]() 或
或![]() 或
或![]() .
.
②∵A型车每辆需租金150元/次,B型车每辆需租金200元/次,
∴当![]() 时,需租金:130×13+200×2=2090元;
时,需租金:130×13+200×2=2090元;
当![]() 时,需租金:130×8+200×5=2040元;
时,需租金:130×8+200×5=2040元;
当![]() 时,需租金:130×3+200×8=1990元,
时,需租金:130×3+200×8=1990元,
∵2090>2040>1990,
所以租车费用最少的是1990元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AB∥DE,AC∥DF,AC=DF下列条件中,不能判断△ABC≌△DEF的是( )

A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.

A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D,E在△ABC的边BC上,AB=AC,AD=AE.
(1)求证:BD=CE;
(2)若AD=BD=DE,求∠BAC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
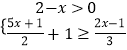 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.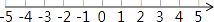
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
在解形如3|x-2|=|x-2|+4这一类含有绝对值的方程时,我们可以根据绝对值的意义分x<2和x≥2两种情况讨论:
①当x<2时,原方程可化为-3(x-2)=-(x-2)+4,解得:x=0,符合x<2
②当x≥2时,原方程可化为3(x-2)=(x-2)+4,解得:x=4,符合x≥2
∴原方程的解为:x=0,x=4.
解题回顾:本题中2为x-2的零点,它把数轴上的点所对应的数分成了x<2和x≥2两部分,所以分x<2和x≥2两种情况讨论.
知识迁移:
(1)运用整体思想先求|x-3|的值,再去绝对值符号的方法解方程:|x-3|+8=3|x-3|;
知识应用:
(2)运用分类讨论先去绝对值符号的方法解类似的方程:|2-x|-3|x+1|=x-9.
(提示:本题中有两个零点,它们把数轴上的点所对应的数分成了几部分呢?)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=5,BC=3,AC=4,点E,F分别是AB,BC的中点.以下结论错误的是( )
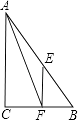
A.△ABC是直角三角形
B.AF是△ABC的中位线
C.EF是△ABC的中位线
D.△BEF的周长为6
相关试题

