【题目】如图,在△ABC中,AB=5,BC=3,AC=4,点E,F分别是AB,BC的中点.以下结论错误的是( )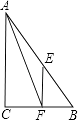
A.△ABC是直角三角形
B.AF是△ABC的中位线
C.EF是△ABC的中位线
D.△BEF的周长为6
参考答案:
【答案】B
【解析】解:A、正确.∵AB=5,BC=3,AC=4,
∴AB2=BC2+AC2,
∴△ACB是直角三角形,故正确.
B、错误.AF是△ABC的中线,不是中位线.
C、正确.∵点E,F分别是AB,BC的中点,
∴EF是△ABC的中位线,故正确.
D、正确.易知EF= ![]() AC=2,EB=
AC=2,EB= ![]() AB=
AB= ![]() ,FB=
,FB= ![]() BC=
BC= ![]() ,
,
∴△EFB的周长=6,故正确,
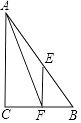
所以答案是:B.
【考点精析】解答此题的关键在于理解勾股定理的逆定理的相关知识,掌握如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形,以及对三角形中位线定理的理解,了解连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:用3辆A型车和2辆B型车载满货物一次可运货共19吨;用2辆A型车和3辆B型车载满货物一次可运货共21吨.
(1)1辆A型车和1辆B型车都载满货物一次分别可以运货多少吨?
(2)某物流公司现有49吨货物,计划同时租用A型车
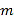 辆,B型车
辆,B型车 辆,一次运完,且恰好每辆车都载满货物.
辆,一次运完,且恰好每辆车都载满货物.①求
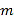 、
、 的值;
的值;②若A型车每辆需租金130元/次,B型车每辆需租金200元/次.请求出租车费用最少是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
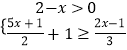 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.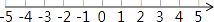
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
在解形如3|x-2|=|x-2|+4这一类含有绝对值的方程时,我们可以根据绝对值的意义分x<2和x≥2两种情况讨论:
①当x<2时,原方程可化为-3(x-2)=-(x-2)+4,解得:x=0,符合x<2
②当x≥2时,原方程可化为3(x-2)=(x-2)+4,解得:x=4,符合x≥2
∴原方程的解为:x=0,x=4.
解题回顾:本题中2为x-2的零点,它把数轴上的点所对应的数分成了x<2和x≥2两部分,所以分x<2和x≥2两种情况讨论.
知识迁移:
(1)运用整体思想先求|x-3|的值,再去绝对值符号的方法解方程:|x-3|+8=3|x-3|;
知识应用:
(2)运用分类讨论先去绝对值符号的方法解类似的方程:|2-x|-3|x+1|=x-9.
(提示:本题中有两个零点,它们把数轴上的点所对应的数分成了几部分呢?)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年10月31日,在广州举行的世界城市日全球主场活动开幕式上,住建部公布许昌成为“国家生态园林城市”在2018年植树节到来之际,许昌某中学购买了甲、乙两种树木用于绿化校园.若购买7棵甲种树和4棵乙种树需510元;购买3棵甲种树和5棵乙种树需350元.
(1)求甲种树和乙种树的单价;
(2)按学校规划,准备购买甲、乙两种树共200棵,且甲种树的数量不少于乙种树的数量的
 ,请设计出最省钱的购买方案,并说明理由.
,请设计出最省钱的购买方案,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的布袋里装有16个只有颜色不同的球,其中红球有x个,白球有2x个,其他均为黄球,现甲从布袋中随机摸出一个球,若是红球则甲同学胜,甲同学把摸出的球放回并搅匀,由乙同学随机摸出一个球,若为黄球,则乙同学胜.
(1)当x=3时,谁获胜的可能性大?
(2)当x为何值时,游戏对双方是公平的?
相关试题

