【题目】如图,二次函数 ![]() 的图象经过坐标原点,与x轴的另一个交点为A(-2,0).
的图象经过坐标原点,与x轴的另一个交点为A(-2,0).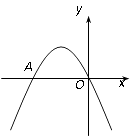
(1)求二次函数的解析式
(2)在抛物线上是否存在一点P,使△AOP的面积为3,若存在请求出点P的坐标,若不存在,请说明理由.
参考答案:
【答案】
(1)解:∵二次函数y=-x2+bx+c的图象经过坐标原点(0,0)
∴c=0.
又∵二次函数y=-x2+bx+c的图象过点A(-2,0)
∴-(-2)2-2b+0=0,
∴b=-2.
∴所求b、c值分别为-2,0
故二次函数解析式为:y=-x2-2x.
(2)解:存在一点P,满足S△AOP=3.
设点P的坐标为(x,-x2-2x)
∵S△AOP=3
∴ ![]() ×2×|-x2-2x|=3
×2×|-x2-2x|=3
∴-x2-2x=±3.
当-x2-2x=3时,此方程无解;
当-x2-2x=-3时,
解得 x1=-3,x2=1.
∴点P的坐标为(-3,-3)或(1,-3)
【解析】(1)抓住已知条件抛物线经过原点(0,0)和A(-2,0).将这两点坐标代入函数解析式,建立方程组,求解即可得到抛物线的解析式。
(2)由于点P在抛物线上,因此设点P的坐标为(x,-x2-2x),根据点A的坐标可求出OA=2,再根据S△AOP=3,建立方程,解方程求出x的值,即可得到点P的坐标。
【考点精析】通过灵活运用因式分解法和三角形的面积,掌握已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势;三角形的面积=1/2×底×高即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=6cm,BC=12cm,∠B=90°.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P,Q分别从A,B同时出发,设移动时间为t(s).

(1)当t=2时,求△PBQ的面积;
(2)当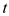 为多少时,四边形APQC的面积最小?最小面积是多少?
为多少时,四边形APQC的面积最小?最小面积是多少?
(3)当 为多少时,△PQB与△ABC相似.
为多少时,△PQB与△ABC相似. -
科目: 来源: 题型:
查看答案和解析>>【题目】圆形钟面上从2点整到4点整,时针和分针成60度角时的时间是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】鲁能巴蜀中学2018年校艺术节“巴蜀好声音”独唱预选赛中,初二年级25名同学的成绩
 满分为10分
满分为10分 统计如下:
统计如下: ,
, ,
, ,
, ,
, ,
, ,
,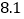 ,
, ,
, ,
, ,
, ,
, ,
,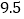 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,10
,10 分及以上为A级,
分及以上为A级, 分为B级
分为B级 包括
包括 分和
分和 分
分 ,
, 分为C级
分为C级 包括
包括 分和
分和 分
分 ,
, 分以下为D级
分以下为D级 请把下面表格补充完整;
请把下面表格补充完整;等级
A
B
C
D
人数
4
8
 级8位同学成绩的中位数是多少,众数是多少;
级8位同学成绩的中位数是多少,众数是多少; 若成绩为A级的同学将参加学校的汇演,请求出初二年级A级同学的平均成绩?
若成绩为A级的同学将参加学校的汇演,请求出初二年级A级同学的平均成绩? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知原点为
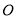 的数轴上,点
的数轴上,点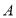 表示的数为-7,点
表示的数为-7,点 表示的数为5.
表示的数为5.
(1)若数轴上点
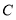 到点
到点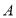 ,点
,点 的距离相等,求点
的距离相等,求点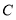 表示的数;
表示的数;(2)若数轴上点
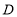 到点
到点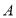 ,到点
,到点 的距离之比为
的距离之比为 ,求点
,求点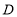 表示的数;
表示的数;(3)若一动点
 从点
从点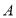 以每秒1个单位长度沿数轴向左匀速运动,同时动点
以每秒1个单位长度沿数轴向左匀速运动,同时动点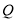 从点
从点 出发,以每秒3个单位长度沿数轴向左匀速运动,设运动的时间为
出发,以每秒3个单位长度沿数轴向左匀速运动,设运动的时间为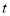 秒
秒 ,
,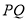 之间的距离为8个单位长度时,求
之间的距离为8个单位长度时,求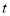 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 的图象如图所示,有以下结论:①
的图象如图所示,有以下结论:①  ;②
;②  ;③
;③ 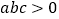 ;④
;④  ;⑤
;⑤  其中所有正确结论的序号是( )
其中所有正确结论的序号是( )
A.①②
B.①③④
C.①②③⑤
D.①②③④⑤ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,给出下列条件:①
 ;②
;②  ;③
;③  ;④
;④  其中单独能够判定
其中单独能够判定  的个数为( )
的个数为( )
A.1
B.2
C.3
D.4
相关试题

