【题目】如图,在△ABC中,AB=6cm,BC=12cm,∠B=90°.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P,Q分别从A,B同时出发,设移动时间为t(s).
(1)当t=2时,求△PBQ的面积;
(2)当 ![]() 为多少时,四边形APQC的面积最小?最小面积是多少?
为多少时,四边形APQC的面积最小?最小面积是多少?
(3)当 ![]() 为多少时,△PQB与△ABC相似.
为多少时,△PQB与△ABC相似.
参考答案:
【答案】
(1)解:当t=2时,AP=2,BQ=4,PB=4,
∴ ![]() =
= ![]() (cm2)
(cm2)
(2)解:∵AP= ![]() ,BQ=2t,PB=6-t,
,BQ=2t,PB=6-t,
∴ ![]() =
= ![]()
= ![]() ,
,
∴当t=3时, ![]() 有最小值27cm2
有最小值27cm2
(3)解:∵△PQB、△ABC是直角三角形,
∴由 ![]() ,即
,即 ![]() ,
,
解得t=3,
由 ![]() ,即
,即 ![]() ,
,
解得t=1.2,
∴当t=1.2或t=3时,△PQB与△ABC相似
【解析】(1)当t=2时,分别根据点P、点Q的运动速度和运动方向求出BP、BQ的长,再根据三角形的面积公式即可求出结果。
(2)先分别用含t的代数式表示出AP、BQ、BP的长,再根据四边形APQC的面积=△ABC的面积-△PBQ的面积,建立函数关系式,然后将此函数解析式化成顶点式,即可求出四边形APQC的面积最小最小值及此时t的值。
(3)分两种情况讨论:当∠A=∠QPB时;当∠A=∠PQB时,根据相似三角形的对应边成比例,建立关于t的方程,解方程求解即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1过点A(0,4),点D(4,0),直线l2:
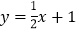 与x轴交于点C,两直线
与x轴交于点C,两直线 ,
, 相交于点B.
相交于点B.(1)求直线
 的解析式和点B的坐标;
的解析式和点B的坐标;(2)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在北京2008年第29届奥运会前夕,某超市在销售中发现:奥运会吉祥物— “福娃”平均每天可售出20套,每件盈利40元。为了迎接奥运会,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存。经市场调查发现:如果每套降价4元,那么平均每天就可多售出8套。要想平均每天在销售吉祥物上盈利1200元,那么每套应降价多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“拼图,推演,得到了整式的乘法的法则和乘法公式.教材第9章头像拼图这样,借助图形往往能把复杂的数学问题变得简明、形象.
(分数运算)
怎样理解
 ?
?
从图形的变化过程可以看出,长方形先被平均分成3份,取其中的2份(涂
 部分);再将涂色部分平均分成5份,取其中4份(涂
部分);再将涂色部分平均分成5份,取其中4份(涂 部分).这样,可看成原长方形被平均分成15份,取出其中8份,所以
部分).这样,可看成原长方形被平均分成15份,取出其中8份,所以 的
的 占原长方形的
占原长方形的 ,即
,即 .
. (尝试推广)
(1)①类比分数运算,猜想
 的结果是____________;(a、b、c、d均为正整数,且
的结果是____________;(a、b、c、d均为正整数,且 ,
, );
);②请用示意图验证①的猜想并用文字简单解释.
(2)①观察下图,填空:
 ____________;
____________;
②若a、b均为正整数且
 ,猜想
,猜想 的运算结果,并用示意图验证你的猜想,同时加以简单的文字解释.
的运算结果,并用示意图验证你的猜想,同时加以简单的文字解释. -
科目: 来源: 题型:
查看答案和解析>>【题目】圆形钟面上从2点整到4点整,时针和分针成60度角时的时间是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】鲁能巴蜀中学2018年校艺术节“巴蜀好声音”独唱预选赛中,初二年级25名同学的成绩
 满分为10分
满分为10分 统计如下:
统计如下: ,
, ,
, ,
, ,
, ,
, ,
,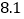 ,
, ,
, ,
, ,
, ,
, ,
,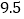 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,10
,10 分及以上为A级,
分及以上为A级, 分为B级
分为B级 包括
包括 分和
分和 分
分 ,
, 分为C级
分为C级 包括
包括 分和
分和 分
分 ,
, 分以下为D级
分以下为D级 请把下面表格补充完整;
请把下面表格补充完整;等级
A
B
C
D
人数
4
8
 级8位同学成绩的中位数是多少,众数是多少;
级8位同学成绩的中位数是多少,众数是多少; 若成绩为A级的同学将参加学校的汇演,请求出初二年级A级同学的平均成绩?
若成绩为A级的同学将参加学校的汇演,请求出初二年级A级同学的平均成绩? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
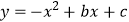 的图象经过坐标原点,与x轴的另一个交点为A(-2,0).
的图象经过坐标原点,与x轴的另一个交点为A(-2,0).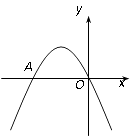
(1)求二次函数的解析式
(2)在抛物线上是否存在一点P,使△AOP的面积为3,若存在请求出点P的坐标,若不存在,请说明理由.
相关试题

