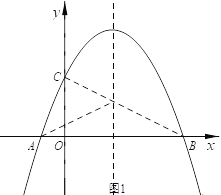
【题目】如图,抛物线经过A(﹣1,0),B(3,0),C(0, ![]() )三点.
)三点.

(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)抛物线的解析式为: ![]() ;
;
(2)P(1,1);
(3)存在,点N的坐标为(2, ![]() ),(
),(![]() ,
, ![]() ),(
),(![]() ,
, ![]() ).
).
【解析】【试题分析】
(1)设抛物线的解析式为y=ax2+bx+c(a≠0),因为A(﹣1,0),B(5,0),C(0, ![]() )三点在抛物线上,则构造三元方程组,得
)三点在抛物线上,则构造三元方程组,得 ,解得
,解得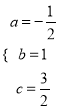 .即抛物线的解析式为:
.即抛物线的解析式为: ![]() ;
;
(2)如图1,根据抛物线的解析式为![]() ,得其对称轴为直线:
,得其对称轴为直线: 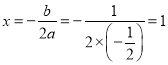 ,连接BC,设直线BC的解析式为
,连接BC,设直线BC的解析式为![]() ,
,
根据B、C两点,得方程组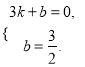 解得
解得
即直线BC的解析式为![]() ,当x=1时,
,当x=1时, ![]() .∴P(1,1);
.∴P(1,1);
(3)存在.A(﹣1,0),C(0, ![]() ),M(m,0),
),M(m,0), ![]() ,根据相对的两个点的中点坐标重合.
,根据相对的两个点的中点坐标重合.
若A、C相对,则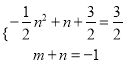 ,解得n=2, ∴N1(2,
,解得n=2, ∴N1(2, ![]() );
);
若A、M相对,则 ,解得n=
,解得n=![]() ∴N2(
∴N2(![]() ,
, ![]() ),N3(
),N3(![]() ,
, ![]() ).;
).;
若A、N相对,则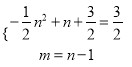 ,解得n=2,(舍去);
,解得n=2,(舍去);
综上所述,点N的坐标为(2, ![]() ),(
),(![]() ,
, ![]() ),(
),(![]() ,
, ![]() ).
).
【试题解析】
(1)设抛物线的解析式为y=ax2+bx+c(a≠0),
∵A(﹣1,0),B(5,0),C(0, ![]() )三点在抛物线上,
)三点在抛物线上,
∴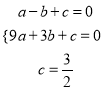 ,解得
,解得 .
.
∴抛物线的解析式为: ![]() ;
;
(2)∵抛物线的解析式为![]() ,
,
∴其对称轴为直线: 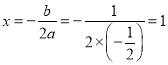 .
.
连接BC,设直线BC的解析式为![]() ,
,
∵B(3,0),C(0, ![]() ),∴
),∴ 解得
解得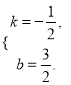
∴直线BC的解析式为![]()
当x=1时, ![]() .∴P(1,1);
.∴P(1,1);
(3)存在.
存在.A(﹣1,0),C(0, ![]() ),M(m,0),
),M(m,0), ![]()
若A、C相对,则 ,解得n=2, ∴N1(2,
,解得n=2, ∴N1(2, ![]() );
);
若A、M相对,则 ,解得n=
,解得n=![]() ∴N2(
∴N2(![]() ,
, ![]() ),N3(
),N3(![]() ,
, ![]() ).;
).;
若A、N相对,则 ,解得n=2,(舍去);
,解得n=2,(舍去);
综上所述,点N的坐标为(2, ![]() ),(
),(![]() ,
, ![]() ),(
),(![]() ,
, ![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查,适合用普查方式的是( )
A. 了解义乌市居民年人均收入B. 了解义乌市民对“低头族”的看法
C. 了解义乌市初中生体育中考的成绩D. 了解某一天离开义乌市的人口流量
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班墙上布置的“学习园地”是一个长方形区域,它的面积为3a2+9ab﹣6a,已知这个长方形“学习园地”的长为3a,则宽为__
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为6,E,F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.

(1)求证:EF=MF;
(2)若AE=2,求FC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商家经销一种绿茶,用于装修门面已投资3000元.已知绿茶每千克成本50元,经研究发现销量y(kg)随销售单价x(元/ kg)的变化而变化,具体变化规律如下表所示:

设该绿茶的月销售利润为w(元)(销售利润=单价×销售量-成本)
(1)请根据上表,求出y与x之间的函数关系式(不必写出自变量x的取值范围);
(2)求w与x之间的函数关系式(不必写出自变量x的取值范围),并求出x为何值时,w的值最大?
(3)若在第一个月里,按使w获得最大值的销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于80元,要想在全部收回装修投资的基础上使第二个月的利润至少达到1700元,那么第二个月时里应该确定销售单价在什么范围内?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
 的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(﹣2,0)及点B.
的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(﹣2,0)及点B.(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足
 ≤kx+b的x的取值范围.
≤kx+b的x的取值范围.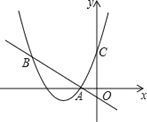
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=50°,∠BOC=30°,则∠AOC= .
相关试题

