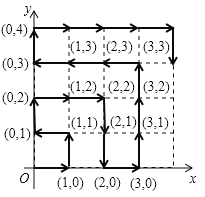
【题目】在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,其对应的点坐标依次为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() …,根据这个规律,第2018个横坐标为( )
…,根据这个规律,第2018个横坐标为( )
A.44B.45C.46D.47
参考答案:
【答案】A
【解析】
根据图形推导出:当n为奇数时,第n个正方形每条边上有(n+1)个点,连同前边所有正方形共有(n+1)2个点,且终点为(0,n);当n为偶数时,第n个正方形每条边上有(n+1)个点,连同前边所以正方形共有(n+1)2个点,且终点为(n,0),然后根据2018=452-7,可推导出452是第几个正方形共有的点,最后再倒推7个点的横坐标即为所求.
解:由图可知:第一个正方形每条边上有2个点,共有4=22个点,且终点为(0,1);
第二个正方形每条边上有3个点,连同第一个正方形共有9=32个点,且终点为(2,0);
第三个正方形每条边上有4个点,连同前两个正方形共有16=42个点,且终点为(0,3);
第四个正方形每条边上有5个点,连同前两个正方形共有25=52个点,且终点为(4,0);
故当n为奇数时,第n个正方形每条边上有(n+1)个点,连同前边所有正方形共有(n+1)2个点,且终点为(0,n);当n为偶数时,第n个正方形每条边上有(n+1)个点,连同前边所以正方形共有(n+1)2个点,且终点为(n,0).
而2018=452-7
n+1=45
解得:n=44
由规律可知,第44个正方形每条边上有45个点,且终点坐标为(44,0),由图可知,再倒着推7个点的横坐标为:44.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中假命题是( )
A.在同一平面内,有三条直线
 、
、 、
、 ,如果
,如果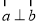 ,
, ,则
,则
B.当被开方数扩大到100倍时,算术平方根的结果扩大到10倍
C.在同一平面内,有三条直线
 、
、 、
、 ,如果
,如果 ,
, ,则
,则
D.直线外一点到这条直线的垂线段的长度,叫做点到直线的距离
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,以△ABC的边AB为直径作⊙O,交AC边于点E,BD平分∠ABE交AC于F,交⊙O于点D,且∠BDE=∠CBE.
(1)求证:BC是⊙O的切线;
(2)延长ED交直线AB于点P,如图2,若PA=AO,DE=3,DF=2,求
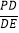 的值及AO的长.
的值及AO的长.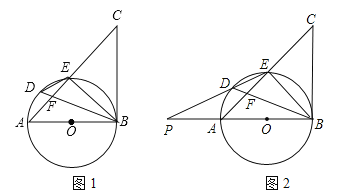
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,ABCD为正方形,将正方形的边CB绕点C顺时针旋转到CE,记∠BCE=α,连接BE,DE,过点C作CF⊥DE于F,交直线BE于H.
(1)当α=60°时,如图1,则∠BHC= ;
(2)当45°<α<90°,如图2,线段BH、EH、CH之间存在一种特定的数量关系,请你通过探究,写出这个关系式: (不需证明);
(3)当90°<α<180°,其它条件不变(如图3),(2)中的关系式是否还成立?若成立,说明理由;若不成立,写出你认为成立的结论,并简要证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
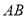 ,
,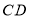 相交于点
相交于点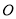 ,
, 平分
平分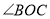 ,
,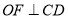 于点
于点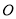 ,
, ,请补全图形,并求出
,请补全图形,并求出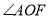 的度数.
的度数.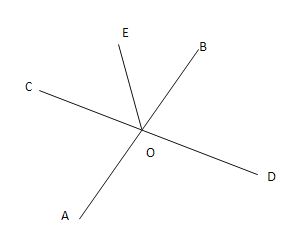
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,D为边BC上一点,E为边AB的中点,过点A作AF∥BC,交DE的延长线于点F,连结BF.
(1)求证:四边形ADBF是平行四边形;
(2)当D为边BC的中点,且BC=2AC时,求证:四边形ACDF为正方形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AD∥BC,AB=CD,BC=10,对角线AC、BD相交于点O,且AC⊥BD,设AD=x,△AOB的面积为y.
(1)求∠DBC的度数;
(2)求y关于x的函数解析式,并写出自变量x的取值范围;
(3)如图1,设点P、Q分别是边BC、AB的中点,分别联结OP,OQ,PQ.如果△OPQ是等腰三角形,求AD的长.

相关试题

