【题目】如图,在△ABC中,∠C=90°,D为边BC上一点,E为边AB的中点,过点A作AF∥BC,交DE的延长线于点F,连结BF.
(1)求证:四边形ADBF是平行四边形;
(2)当D为边BC的中点,且BC=2AC时,求证:四边形ACDF为正方形.

参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据平行线的性质得到∠AFE=∠BDE,根据全等三角形的性质得到AF=BD,于是得到结论;
(2)首先证明四边形ACDF是矩形,再证明CA=CD即可解决问题;
(1)证明:∵AF∥BC,
∴∠AFE=∠BDE,
在△AEF与△BED中,
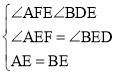 ,
,
∴△AEF≌△BED,
∴AF=BD,
∵AF∥BD,
∴四边形ADBF是平行四边形;
(2)解:∵CD=DB,AE=BE,
∴DE∥AC,
∴∠FDB=∠C=90°,
∵AF∥BC,
∴∠AFD=∠FDB=90°,
∴∠C=∠CDF=∠AFD=90°,
∴四边形ACDF是矩形,
∵BC=2AC,CD=BD,
∴CA=CD,
∴四边形ACDF是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,ABCD为正方形,将正方形的边CB绕点C顺时针旋转到CE,记∠BCE=α,连接BE,DE,过点C作CF⊥DE于F,交直线BE于H.
(1)当α=60°时,如图1,则∠BHC= ;
(2)当45°<α<90°,如图2,线段BH、EH、CH之间存在一种特定的数量关系,请你通过探究,写出这个关系式: (不需证明);
(3)当90°<α<180°,其它条件不变(如图3),(2)中的关系式是否还成立?若成立,说明理由;若不成立,写出你认为成立的结论,并简要证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,其对应的点坐标依次为
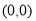 ,
,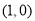 ,
,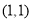 ,
,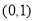 ,
,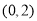 ,
,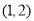 ,
,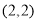 ,
, …,根据这个规律,第2018个横坐标为( )
…,根据这个规律,第2018个横坐标为( )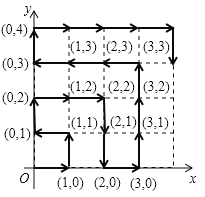
A.44B.45C.46D.47
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
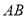 ,
,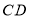 相交于点
相交于点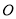 ,
, 平分
平分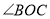 ,
,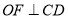 于点
于点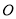 ,
, ,请补全图形,并求出
,请补全图形,并求出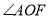 的度数.
的度数.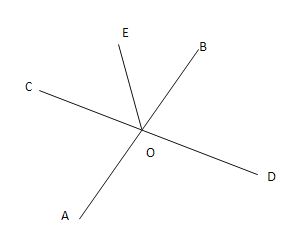
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AD∥BC,AB=CD,BC=10,对角线AC、BD相交于点O,且AC⊥BD,设AD=x,△AOB的面积为y.
(1)求∠DBC的度数;
(2)求y关于x的函数解析式,并写出自变量x的取值范围;
(3)如图1,设点P、Q分别是边BC、AB的中点,分别联结OP,OQ,PQ.如果△OPQ是等腰三角形,求AD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的正方形网格中,每个小正方形的边长均为1个单位长度,三角形
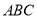 的三个顶点都在格点上.
的三个顶点都在格点上.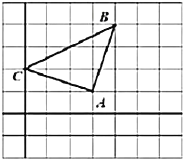
(1)请你以
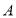 为原点
为原点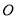 ,建立平面直角坐标系,并写出
,建立平面直角坐标系,并写出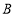 、
、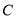 两点的坐标.
两点的坐标.(2)若三角形
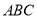 内部有一点
内部有一点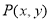 ,经过平移后的对应点
,经过平移后的对应点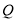 的坐标为
的坐标为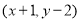 ,且
,且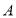 、
、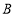 、
、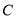 的对应点分别为
的对应点分别为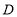 、
、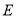 、
、 ,请说明三角形
,请说明三角形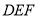 是如何由三角形
是如何由三角形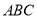 平移得到(沿网格线平移),并画出三角形
平移得到(沿网格线平移),并画出三角形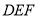 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数的图象经过
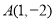 ,
,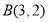 两点.
两点.(1)求这个一次函数的解析式;
(2)试判断点
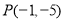 是否在这个一次函数的图象上;
是否在这个一次函数的图象上;(3)求此函数图象与
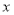 轴,
轴, 轴围成的三角形的面积.
轴围成的三角形的面积.
相关试题

