【题目】如图,抛物线y= ![]() x2+bx+c与y轴交于点C(0,﹣4),与x轴交于点A、B,且B点的坐标为(2,0).
x2+bx+c与y轴交于点C(0,﹣4),与x轴交于点A、B,且B点的坐标为(2,0).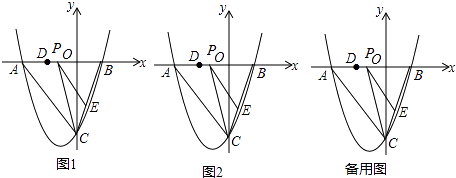
(1)求抛物线的解析式;
(2)若点P是AB上的一个动点,过点P作PE∥AC交BC于点E,连接CP,求△PCE面积最大时P点的坐标;
(3)在(2)的条件下,若点D为OA的中点,点M是线段AC上一点,当△OMD为等腰三角形时,连接MP、ME,把△MPE沿着PE翻折,点M的对应点为点N,直接写出点N的坐标.
参考答案:
【答案】
(1)
解:根据题意得:
![]() ,
,
解得: ![]() ,
,
所以该抛物线的解析式为:y= ![]() x2+x﹣4;
x2+x﹣4;
(2)
解:令y=0,即 ![]() x2+x﹣4=0,解得x1=﹣4,x2=2,
x2+x﹣4=0,解得x1=﹣4,x2=2,
∴A(﹣4,0),S△ABC= ![]() ABOC=12
ABOC=12
设P点坐标为(x,0),则PB=2﹣x.
∵PE∥BC,
∴∠BPE=∠BAC,∠BEP=∠BCA,
∴△PBE∽△BAC,
∴ ![]() =(
=( ![]() )2,即
)2,即 ![]() =(
=( ![]() )2,
)2,
化简得:S△PBE= ![]() (2﹣x)2.
(2﹣x)2.
S△PCE=S△PCB﹣S△PBE= ![]() PBOC﹣S△PBE=
PBOC﹣S△PBE= ![]() ×(2﹣x)×4﹣
×(2﹣x)×4﹣ ![]() (2﹣x)2
(2﹣x)2
=﹣ ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() =﹣
=﹣ ![]() (x+1)2+3
(x+1)2+3
∴当x=﹣1时,S△PCE的最大值为3.
(3)
解:由(2)已知A(﹣4,0),
∵点D为0A中点,
∴D(﹣2,0),
设直线AC的解析式为y=mx+n,
把A(﹣4,0)、C(0,﹣4)分别代入得:
![]() ,解得
,解得 ![]() ,
,
∴直线AC的解析式为y=﹣x﹣4.
∵PE∥AC,所以可设直线PE的解析式为y=﹣x+a,
将P(﹣1,0)代入y=﹣x﹣a得a=﹣1,
所以直线PE的解析式为y=﹣x﹣1.
设直线BC的解析式为y=kx+a′,
将B(2,0)、C(0,﹣4)代入y=kx+a′得 ![]() ,
,
解得k=2,a′=﹣4.
所以直线BC的解析式为y=2x﹣4.
由2x﹣4=﹣x﹣1得x=1,将x=1代入y=2x﹣4得y=﹣2,
∴E点坐标为(1,﹣2).
①当MD=OD时,如图1:
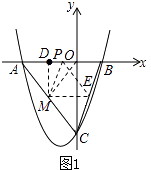
∵AD=MD=AD,OA=OC,∠DAM=∠OAC,
∴△ADM∽△AOC,
∴∠ADM=∠AOC=90°,即DM⊥x轴,
<>∴M的横坐标为﹣2,将x=﹣2代入y=﹣x﹣4,得y=﹣2.所以此时M的坐标为(﹣2,﹣2);
∵M和E点纵坐标相等,
∴ME∥x轴,
∴∠PEM=45°.
由翻折得∠ENM=2∠PEM=90°,即NE∥y轴,
∴EN=ME=3,
∵E(1,﹣2),
∴N(1,1).
②当DM=OM时,过点M作MG⊥x轴交于点,如图2:
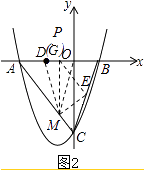
易知DG=OG=1,即G点与P点重合,M的横坐标为﹣1,
将x=﹣1代入y=﹣x﹣4,得y=﹣3.
∴M(﹣1,﹣3).
∵ME= ![]() =
= ![]() ,EB=
,EB= ![]() =
= ![]() ,
,
∴ME=EB,
∵PB=3,PM=3,即PB=PM,
又∵PE=PE,
∴△BPE≌△MPE,
∴∠BEP=∠MEP,
∴点N与点B重合,
∴N(2,0);
③当OD=OM时,
设点O到AC的最短距离为h,则OAOC=hAC
∵AC= ![]() =
= ![]() =4
=4 ![]() ,
,
∴h= ![]() =2
=2 ![]() ,
,
∵h>OD,
∴OD≠OM.此时等腰△OMD不存在.
综上所述,N点的坐标分别为(1,1)或(2,0).
【解析】(1)把B点和C点坐标分别代入y= ![]() x2+bx+c得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线解析式;(2)首先求出△PCE面积的表达式,然后利用二次函数的性质求出其最大值;(3)易知D(﹣2,0),接着利用待定系数求出直线AC的解析式为y=﹣x﹣4,再根据直线PE与直线BC的解析式求得点E的坐标为(1,﹣2).求M点分类讨论:①当MD=OD时,求得M的坐标为(﹣2,﹣2);所以ME∥x轴,则∠PEM=45°,由翻折得∠NEM=90°,所以NE∥y轴,可得N(1,1);②当DM=OM时,求得M的坐标为(﹣1,﹣3),又可证得△MPE≌△BPE,所以N与B重合,N点坐标为(2,0);③OD=OM时,等腰△OMD不存在.
x2+bx+c得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线解析式;(2)首先求出△PCE面积的表达式,然后利用二次函数的性质求出其最大值;(3)易知D(﹣2,0),接着利用待定系数求出直线AC的解析式为y=﹣x﹣4,再根据直线PE与直线BC的解析式求得点E的坐标为(1,﹣2).求M点分类讨论:①当MD=OD时,求得M的坐标为(﹣2,﹣2);所以ME∥x轴,则∠PEM=45°,由翻折得∠NEM=90°,所以NE∥y轴,可得N(1,1);②当DM=OM时,求得M的坐标为(﹣1,﹣3),又可证得△MPE≌△BPE,所以N与B重合,N点坐标为(2,0);③OD=OM时,等腰△OMD不存在.
【考点精析】本题主要考查了相似三角形的应用的相关知识点,需要掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数
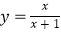 的图象与性质.小怀根据学习函数的经验,对函数
的图象与性质.小怀根据学习函数的经验,对函数 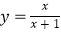 的图象与性质进行了探究.下面是小怀的探究过程,请补充完成:
的图象与性质进行了探究.下面是小怀的探究过程,请补充完成:
(1)函数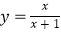 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)列出y与x的几组对应值.请直接写出m的值,m=;
(3)请在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)结合函数的图象,写出函数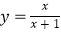 的一条性质.
的一条性质. x
…
﹣5
﹣4
﹣3
﹣2
﹣

﹣

0
1
2
m
4
5
…
y
…



2
3
﹣1
0



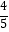

…
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们把两条中线互相垂直的三角形称为“中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均为“中垂三角形”,设BC=a,AC=b,AB=c.
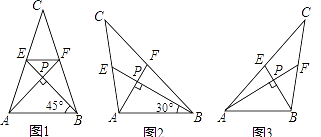
(1)【特例探索】
如图1,当∠ABE=45°,c=2 时,a= , b=;如图2,当∠ABE=30°,c=4时,a= , b=;
时,a= , b=;如图2,当∠ABE=30°,c=4时,a= , b=;
(2)【归纳证明】
请你观察(1)中的计算结果,猜想a2 , b2 , c2三者之间的关系,用等式表示出来,请利用图3证明你发现的关系式;
(3)【拓展应用】
如图4,在ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=2 ,AB=3.求AF的长.
,AB=3.求AF的长.
-
科目: 来源: 题型:
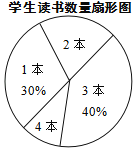
查看答案和解析>>【题目】某校七年级共有500名学生,在“世界读书日”前夕,开展了“阅读助我成长”的读书活动.为了解该年级学生在此次活动中课外阅读情况,童威随机抽取m名学生,调查他们课外阅读书籍的数量,将收集的数据整理成如下统计表和扇形图.
学生读书数量统计表
阅读量/本
学生人数
1
15
2
a
3
b
4
5
(1)直接写出m、a、b的值;
(2)估计该年级全体学生在这次活动中课外阅读书籍的总量大约是多少本?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小慧根据学习函数的经验,对函数
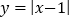 的图像与性质进行了探究.下面是小慧的探究过程,请补充完整.
的图像与性质进行了探究.下面是小慧的探究过程,请补充完整.(l)函数
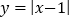 的自变量
的自变量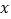 的取值范围是 ;
的取值范围是 ;(2)列表,找出
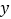 与
与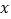 的几组对应值.
的几组对应值.
其中,
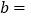 ;
;(3)在平面直角坐标系
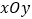 中,描出以上表中各对对应值为坐标的点,并画出该函数的图像;
中,描出以上表中各对对应值为坐标的点,并画出该函数的图像;(4)写出该函数的一条性质: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t
频数
百分比
2≤x<3
2
4%
3≤x<4
12
24%
4≤x<5
5≤x<6
10
20%
6≤x<7
12%
7≤x<8
3
6%
8≤x<9
2
4%

(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
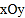 中,
中, ,直线
,直线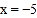 与
与 轴交于点
轴交于点 ,直线
,直线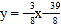 与
与 轴及直线
轴及直线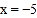 分别交于点
分别交于点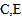 .点
.点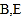 关于
关于 轴对称,连接
轴对称,连接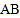 .
.(1)求点
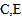 的坐标及直线
的坐标及直线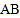 的表达式;
的表达式;(2)设面积的和
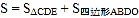 ,求
,求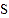 的值;
的值;(3)在求(2)中
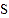 时,嘉琪有个想法:“将
时,嘉琪有个想法:“将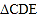 沿
沿 轴翻折到
轴翻折到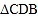 的位置,
的位置,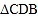 与四边形
与四边形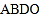 拼接后可看成
拼接后可看成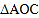 ,这样求
,这样求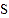 便转化为直接求
便转化为直接求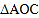 的面积不更快捷吗?”但大家经反复验算,发现
的面积不更快捷吗?”但大家经反复验算,发现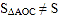 ,请通过计算解释他的想法错在哪里.
,请通过计算解释他的想法错在哪里.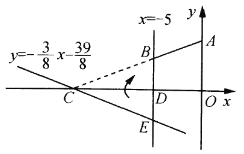
相关试题

