【题目】如图,在平面直角坐标系![]() 中,
中,![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴及直线
轴及直线![]() 分别交于点
分别交于点![]() .点
.点![]() 关于
关于![]() 轴对称,连接
轴对称,连接![]() .
.
(1)求点![]() 的坐标及直线
的坐标及直线![]() 的表达式;
的表达式;
(2)设面积的和![]() ,求
,求![]() 的值;
的值;
(3)在求(2)中![]() 时,嘉琪有个想法:“将
时,嘉琪有个想法:“将![]() 沿
沿![]() 轴翻折到
轴翻折到![]() 的位置,
的位置,![]() 与四边形
与四边形![]() 拼接后可看成
拼接后可看成![]() ,这样求
,这样求![]() 便转化为直接求
便转化为直接求![]() 的面积不更快捷吗?”但大家经反复验算,发现
的面积不更快捷吗?”但大家经反复验算,发现![]() ,请通过计算解释他的想法错在哪里.
,请通过计算解释他的想法错在哪里.
参考答案:
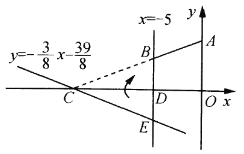
【答案】(1)C(-13,0),E(-5,-3),![]() ;(2)32;(3)见解析.
;(2)32;(3)见解析.
【解析】
(1)利用坐标轴上点的特点确定出点C的坐标,再利用直线的交点坐标的确定方法求出点E坐标,进而得到点B坐标,最后用待定系数法求出直线AB解析式;
(2)直接利用直角三角形的面积计算方法和直角梯形的面积的计算即可得出结论,
(3)先求出直线AB与x轴的交点坐标,判断出点C不在直线AB上,即可.
(1)在直线![]() 中,令y=0,则有0=
中,令y=0,则有0=![]() ,
,
∴x=﹣13,
∴C(﹣13,0),
令x=﹣5,代入![]() ,解得y=﹣3,
,解得y=﹣3,
∴E(﹣5,﹣3),
∵点B,E关于x轴对称,
∴B(﹣5,3),
∵A(0,5),
∴设直线AB的解析式为y=kx+5,
∴﹣5k+5=3,
∴k=![]() ,
,
∴直线AB的解析式为![]() ;
;
(2)由(1)知E(﹣5,﹣3),
∴DE=3,
∵C(﹣13,0),
∴CD=﹣5﹣(﹣13)=8,
∴S△CDE=![]() CD×DE=12,
CD×DE=12,
由题意知,OA=5,OD=5,BD=3,
∴S四边形ABDO=![]() (BD+OA)×OD=20,
(BD+OA)×OD=20,
∴S=S△CDE+S四边形ABDO=12+20=32;
(3)由(2)知,S=32,
在△AOC中,OA=5,OC=13,
∴S△AOC=![]() OA×OC=
OA×OC=![]() =32.5,
=32.5,
∴S≠S△AOC,
理由:由(1)知,直线AB的解析式为![]() ,令y=0,则0=
,令y=0,则0=![]() ,
,
∴x=﹣![]() ≠﹣13,
≠﹣13,
∴点C不在直线AB上,
即:点A,B,C不在同一条直线上,
∴S△AOC≠S.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
 x2+bx+c与y轴交于点C(0,﹣4),与x轴交于点A、B,且B点的坐标为(2,0).
x2+bx+c与y轴交于点C(0,﹣4),与x轴交于点A、B,且B点的坐标为(2,0).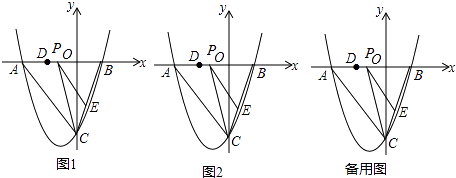
(1)求抛物线的解析式;
(2)若点P是AB上的一个动点,过点P作PE∥AC交BC于点E,连接CP,求△PCE面积最大时P点的坐标;
(3)在(2)的条件下,若点D为OA的中点,点M是线段AC上一点,当△OMD为等腰三角形时,连接MP、ME,把△MPE沿着PE翻折,点M的对应点为点N,直接写出点N的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】小慧根据学习函数的经验,对函数
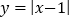 的图像与性质进行了探究.下面是小慧的探究过程,请补充完整.
的图像与性质进行了探究.下面是小慧的探究过程,请补充完整.(l)函数
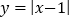 的自变量
的自变量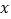 的取值范围是 ;
的取值范围是 ;(2)列表,找出
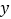 与
与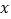 的几组对应值.
的几组对应值.
其中,
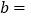 ;
;(3)在平面直角坐标系
 中,描出以上表中各对对应值为坐标的点,并画出该函数的图像;
中,描出以上表中各对对应值为坐标的点,并画出该函数的图像;(4)写出该函数的一条性质: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t
频数
百分比
2≤x<3
2
4%
3≤x<4
12
24%
4≤x<5
5≤x<6
10
20%
6≤x<7
12%
7≤x<8
3
6%
8≤x<9
2
4%

(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y是x的反比例函数,且x=8时,y=12.
(1)写出y与x之间的函数关系式;
(2)如果自变量x的取值范围是2≤x≤3,求y的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=90°,BC=
 .以BC的中点O为圆心的圆分别与AB、AC相切于D、E两点,则
.以BC的中点O为圆心的圆分别与AB、AC相切于D、E两点,则  的长为 ( )
的长为 ( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“中国梦”是中华民族每一个人的梦,也是每一个中小学生的梦,各中小学开展经典诵读活动,无疑是“中国梦”教育这一宏大乐章里的响亮音符,学校在经典诵读活动中,对全校学生用A、B、C、D四个等级进行评价,现从中抽取若干个学生进行调查,绘制出了两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)共抽取了多少个学生进行调查?
(2)将图甲中的折线统计图补充完整.
(3)求出图乙中B等级所占圆心角的度数.

相关试题

