【题目】我们把两条中线互相垂直的三角形称为“中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均为“中垂三角形”,设BC=a,AC=b,AB=c.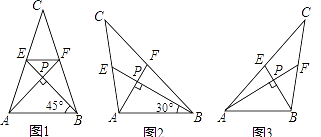
(1)【特例探索】
如图1,当∠ABE=45°,c=2 ![]() 时,a= , b=;如图2,当∠ABE=30°,c=4时,a= , b=;
时,a= , b=;如图2,当∠ABE=30°,c=4时,a= , b=;
(2)【归纳证明】
请你观察(1)中的计算结果,猜想a2 , b2 , c2三者之间的关系,用等式表示出来,请利用图3证明你发现的关系式;
(3)【拓展应用】
如图4,在ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=2 ![]() ,AB=3.求AF的长.
,AB=3.求AF的长.
参考答案:
【答案】
(1)2 ![]() ;2
;2 ![]() ;2
;2 ![]() ;2
;2 ![]()
(2)
猜想:a 2,b2,c2三者之间的关系是:a2+b2=5c2,
证明:如图3,连接EF,
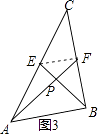
∵AF,BE是△ABC的中线,
∴EF是△ABC的中位线,
∴EF∥AB.且 EF= ![]() AB=
AB= ![]() c.
c.
∴ ![]()
设 PF=m,PE=n 则AP=2m,PB=2n,
在Rt△APB中,(2m)2+(2n)2=c2①
在Rt△APE中,(2m)2+n2=( ![]() )2②
)2②
在Rt△BPF中,m2+(2n)2=( ![]() )2③
)2③
由①得:m2+n2= ![]() ,由②+③得:5( m2+n2)=
,由②+③得:5( m2+n2)= ![]() ,
,
∴a 2+b2=5 c2;
(3)
如图4,连接AC,EF交于H,AC与BE交于点Q,设BE与AF的交点为P,
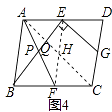
∵点E、G分别是AD,CD的中点,
∴EG∥AC,
∵BE⊥EG,
∴BE⊥AC,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=2 ![]() ,
,
∴∠EAH=∠FCH,
∵E,F分别是AD,BC的中点,
∴AE= ![]() AD,BF=
AD,BF= ![]() BC,
BC,
∴AE=BF=CF= ![]() AD=
AD= ![]() ,
,
∵AE∥BF,
∴四边形ABFE是平行四边形,
∴EF=AB=3,AP=PF,
在△AEH和△CFH中, 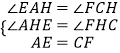 ,
,
∴△AEH≌△CFH,
∴EH=FH,
∴EP,AH分别是△AFE的中线,
由(2)的结论得:AF2+EF2=5AE2,
∴AF2=5( ![]() )2﹣EF2=16,
)2﹣EF2=16,
∴AF=4.
【解析】解:(1.)∵AF⊥BE,∠ABE=45°,
∴AP=BP= ![]() AB=2,
AB=2,
∵AF,BE是△ABC的中线,
∴EF∥AB,EF= ![]() AB=
AB= ![]() ,
,
∴∠PFE=∠PEF=45°,
∴PE=PF=1,
在Rt△FPB和Rt△PEA中,
AE=BF= ![]() =
= ![]() ,
,
∴AC=BC=2 ![]() ,
,
∴a=b=2 ![]() ,
,
如图2,连接EF,
同理可得:EF= ![]() ×4=2,
×4=2,
∵EF∥AB,
∴△PEF~△ABP,
∴ ![]() ,
,
在Rt△ABP中,
AB=4,∠ABP=30°,
∴AP=2,PB=2 ![]() ,
,
∴PF=1,PE= ![]() ,
,
在Rt△APE和Rt△BPF中,
AE= ![]() ,BF=
,BF= ![]() ,
,
∴a=2 ![]() ,b=2
,b=2 ![]() ,
,
所以答案是:2 ![]() ,2
,2 ![]() ,2
,2 ![]() ,2
,2 ![]() ;
;
【考点精析】解答此题的关键在于理解三角形的“三线”的相关知识,掌握1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内,以及对相似三角形的应用的理解,了解测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某经销商销售一种产品,这种产品的成本价为10元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克,且10≤x≤18)之间的函数关系如图所示;
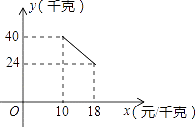
(1)求y(千克)与销售价x的函数关系式;
(2)该经销商想要获得150元的销售利润,销售价应定为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小方格都是边长为1的正方形,我们把以格点连线为边的多边形称为“格点多边形”.如图①中四边形
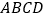 就是一个“格点四边形”.
就是一个“格点四边形”.(1)作出四边形
 关于直线
关于直线 对称的四边形
对称的四边形 ;
;(2)图①中四边形
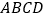 的面积是;
的面积是;(3)在图②方格纸中画一个格点三角形
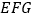 ,使
,使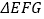 的面积等于8且
的面积等于8且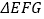 为轴对称.
为轴对称.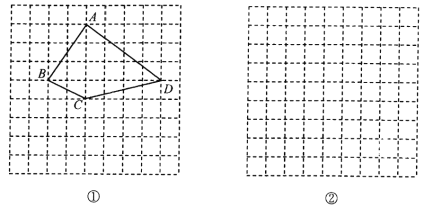
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数
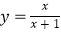 的图象与性质.小怀根据学习函数的经验,对函数
的图象与性质.小怀根据学习函数的经验,对函数 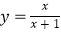 的图象与性质进行了探究.下面是小怀的探究过程,请补充完成:
的图象与性质进行了探究.下面是小怀的探究过程,请补充完成:
(1)函数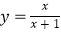 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)列出y与x的几组对应值.请直接写出m的值,m=;
(3)请在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)结合函数的图象,写出函数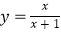 的一条性质.
的一条性质. x
…
﹣5
﹣4
﹣3
﹣2
﹣

﹣

0
1
2
m
4
5
…
y
…



2
3
﹣1
0



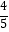

…
-
科目: 来源: 题型:
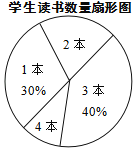
查看答案和解析>>【题目】某校七年级共有500名学生,在“世界读书日”前夕,开展了“阅读助我成长”的读书活动.为了解该年级学生在此次活动中课外阅读情况,童威随机抽取m名学生,调查他们课外阅读书籍的数量,将收集的数据整理成如下统计表和扇形图.
学生读书数量统计表
阅读量/本
学生人数
1
15
2
a
3
b
4
5
(1)直接写出m、a、b的值;
(2)估计该年级全体学生在这次活动中课外阅读书籍的总量大约是多少本?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
 x2+bx+c与y轴交于点C(0,﹣4),与x轴交于点A、B,且B点的坐标为(2,0).
x2+bx+c与y轴交于点C(0,﹣4),与x轴交于点A、B,且B点的坐标为(2,0).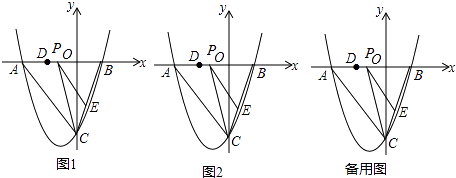
(1)求抛物线的解析式;
(2)若点P是AB上的一个动点,过点P作PE∥AC交BC于点E,连接CP,求△PCE面积最大时P点的坐标;
(3)在(2)的条件下,若点D为OA的中点,点M是线段AC上一点,当△OMD为等腰三角形时,连接MP、ME,把△MPE沿着PE翻折,点M的对应点为点N,直接写出点N的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】小慧根据学习函数的经验,对函数
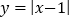 的图像与性质进行了探究.下面是小慧的探究过程,请补充完整.
的图像与性质进行了探究.下面是小慧的探究过程,请补充完整.(l)函数
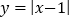 的自变量
的自变量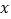 的取值范围是 ;
的取值范围是 ;(2)列表,找出
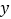 与
与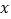 的几组对应值.
的几组对应值.
其中,
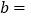 ;
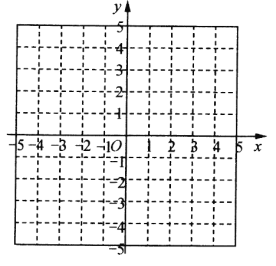
;(3)在平面直角坐标系
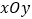 中,描出以上表中各对对应值为坐标的点,并画出该函数的图像;
中,描出以上表中各对对应值为坐标的点,并画出该函数的图像;(4)写出该函数的一条性质: .
相关试题

