搜索
【题目】某工厂生产的某种产品按质量分为1 0个档次．第1档次(最低档次)的产品一天能生产7 6件，每件利润10元．每提高一个档次，每件利润增加2元，但一天产量减少4件．若生产第x档次的产品一天的总利润为1080元，求该产品的质量档次。
参考答案：
【答案】5
【解析】试题分析：首先设产品的质量档次为x，根据题意可得：产品的利润为[10+2（x-1）]元，数量的个数为[76-4（x-1)]个，然后根据总利润=单件利润×数量列出方程求出x的值，然后根据x的取值范围得出x的值，从而得到答案.
试题解析：设该产品的质量档次为x档，根据题意，得[10+2（x-1）][76-4（x-1)]=1080
解得：
=5，
=11 ∵x≤10 ∴x=5
答: 略该产品的质量档次为5.
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
（1）（﹣a3）4（﹣a）3
（2）（﹣x6）﹣（﹣3x3）2+8[﹣（﹣x）3]2
（3）（m2n）3（﹣m4n）+（﹣mn）2
-
科目： 来源： 题型：
查看答案和解析>>【题目】某地计划用120～180天(含120与180天)的时间建设一项水利工程，工程需要运送的土石方总量为360万立方米．
(1)写出运输公司完成任务所需的时间y(单位：天)与平均每天的工作量x(单位：万立方米)之间的函数关系式，并给出自变量x的取值范围；
(2)由于工程进度的需要，实际平均每天运送土石方比原计划多5000立方米，工期比原计划减少了24天，原计划和实际平均每天运送土石方各是多少万立方米？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，AB∥CD，∠BCD＝90°，AB＝AD＝10cm，BC＝8cm．点P从点A出发，以3cm／s的速度沿折线ABCD方向运动，点Q从点D出发，以2cm／s的速度沿线段DC向点C运动．已知P，Q两点同时出发，当点Q到达点C时，P，Q停止运动，设运动时间为t（s）．
(1)、求CD的长．
(2)、当四边形PBQD为平行四边形时，求四边形PBQD的周长．
(3)、当点P在折线BCD上运动时，是否存在某一时刻，使得△BPQ的面积为16cm2？若存在，请求出满足条件的t的值；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=kx+6与x、y轴分别交于E、F．点E坐标为（﹣8，0），点A的坐标为（﹣6，0），P（x，y）是直线y=kx+6上的一个动点．
（1）求k的值；
（2）若点P是第二象限内的直线上的一个动点，当点P运动过程中，试写出三角形OPA的面积S与x的函数关系式，并写出自变量x的取值范围；
（3）探究：当P运动到什么位置时，三角形OPA的面积为
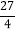，并说明理由．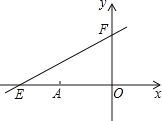
-
科目： 来源： 题型：
查看答案和解析>>【题目】共享单车为市民出行带来了方便，某单车公式第一个月投放a辆单车，计划第三个月投放单车y辆，设该公司第二、三两个月投放单车数量的月平均增长率为x，那么y与x的函数关系是（ ）
A. y=a（1+x）2 B. y=a（1﹣x）2 C. y=（1﹣x）2+a D. y=x2+a
-
科目： 来源： 题型：
查看答案和解析>>【题目】9的平方根是（ ）
A.±3
B.3
C.81
D.±81
相关试题
