Question

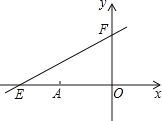
【题目】如图，直线y=kx+6与x、y轴分别交于E、F．点E坐标为（﹣8，0），点A的坐标为（﹣6，0），P（x，y）是直线y=kx+6上的一个动点．

（1）求k的值；

（2）若点P是第二象限内的直线上的一个动点，当点P运动过程中，试写出三角形OPA的面积S与x的函数关系式，并写出自变量x的取值范围；

（3）探究：当P运动到什么位置时，三角形OPA的面积为，并说明理由．

Answer 1

【答案】（1）k的值为；

（2）三角形OPA的面积S与x的函数关系式为S=x+18（﹣8＜x＜0）；

（3）当点P的坐标为P（﹣5，）或P（﹣11，﹣）时，三角形OPA的面积为．

【解析】试题分析: （1）将点E的坐标（-8，0）代入直线y=kx+6，得到关于k的方程，解方程即可求出k的值；

（2）由点A的坐标为（-6，0）得到OA=6，求△OPA的面积时，可看作以OA为底边，高是P点的纵坐标的绝对值．再根据三角形的面积公式表示出△OPA的面积，从而求出其关系式；根据P点运动的范围可求出自变量x的取值范围；

（3）根据三角形的面积公式，由△OPA的面积为，列出关于点P的纵坐标y的方程，解方程求出y的值，再代入直线的解析式求出x的值，即可得到P点的坐标．

试题解析:

（1）∵点E（﹣8，0）在直线y=kx+6上，

∴0=﹣8k+6，∴k=；

（2）∵k=，∴直线的解析式为：y=x+6，

∵点P（x，y）是第二象限内的直线y=x+6上的一个动点，

∴y=x+6＞0，﹣8＜x＜0．

∵点A的坐标为（﹣6，0），

∴OA=6，

∴S=OA|yP|=×6×（x+6）=x+18．

∴三角形OPA的面积S与x的函数关系式为：S=x+18（﹣8＜x＜0）；

（3）∵三角形OPA的面积=OA|yP|=，P（x，y），

∴×6×|y|=，

解得|y|=，

∴y=±．

当y=时，=x+6，

解得x=﹣5，故P（﹣5，）；

当y=﹣时，﹣=x+6，

解得x=﹣11，故P（﹣11，﹣）；

综上可知，当点P的坐标为P（﹣5，）或P（﹣11，﹣）时，三角形OPA的面积为 ．

点睛:此题属于一次函数综合题,涉及 的知识有:待定系数法求一次函数解析式,三角形面积,坐标与图形性质,熟练掌握待定系数法是解本题的关键.