【题目】如图,已知A1 , A2 , A3 , …,An是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1 , A2 , A3 , …,An+1作x轴的垂线交一次函数 ![]() 的图象于点B1 , B2 , B3 , …,Bn+1 , 连接A1B2 , B1A2 , A2B3 , B2A3 , …,AnBn+1 , BnAn+1依次产生交点P1 , P2 , P3 , …,Pn , 则Pn的坐标是 .
的图象于点B1 , B2 , B3 , …,Bn+1 , 连接A1B2 , B1A2 , A2B3 , B2A3 , …,AnBn+1 , BnAn+1依次产生交点P1 , P2 , P3 , …,Pn , 则Pn的坐标是 . 
参考答案:
【答案】(n+ ![]() ,
, ![]() )
)
【解析】解:由已知得A1 , A2 , A3 , …的坐标为:(1,0),(2,0),(3,0),…,
又得作x轴的垂线交一次函数y= ![]() x的图象于点B1 , B2 , B3 , …的坐标分别为(1,
x的图象于点B1 , B2 , B3 , …的坐标分别为(1, ![]() ),(2,1),(3,
),(2,1),(3, ![]() ),….
),….
由此可推出An , Bn , An+1 , Bn+1四点的坐标为,(n,0),(n, ![]() ),(n+1,0),(n+1,
),(n+1,0),(n+1, ![]() ).
).
所以得直线AnBn+1和An+1Bn的直线方程分别为:
y﹣0= ![]() (x﹣n)+0,
(x﹣n)+0,
y﹣0= ![]() (x﹣n﹣1)+0,
(x﹣n﹣1)+0,
即  ,
,
解得: ,
,
所以答案是:(n+ ![]() ,
, ![]() ).
).
【考点精析】掌握数与式的规律是解答本题的根本,需要知道先从图形上寻找规律,然后验证规律,应用规律,即数形结合寻找规律.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线与x轴交于A(x1 , 0)、B(x2 , 0)两点,且x1<x2 , 与y轴交于点C(0,﹣4),其中x1 , x2是方程x2﹣4x﹣12=0的两个根.

(1)求抛物线的解析式;
(2)点M是线段AB上的一个动点,过点M作MN∥BC,交AC于点N,连接CM,当△CMN的面积最大时,求点M的坐标;
(3)点D(4,k)在(1)中抛物线上,点E为抛物线上一动点,在x轴上是否存在点F,使以A、D、E、F为顶点的四边形是平行四边形?如果存在,求出所有满足条件的点F的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】西海岸旅游旺季到来,为应对越来越严峻的交通形势,新区对某道路进行拓宽改造.工程队在工作了一段时间后,因雨被迫停工几天,随后工程队加快了施工进度,按时完成了拓宽改造任务.下面能反映该工程尚未改造的道路y(米)与时间x(天)的函数关系的大致图象是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=﹣x+1与反比例函数
 ,x与y的对应值如下表:
,x与y的对应值如下表: x
﹣3
﹣2
﹣1
1
2
3
y=﹣x+1
4
3
2
0
﹣1
﹣2


1
2
﹣2
﹣1
﹣

不等式﹣x+1>﹣
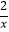 的解为 .
的解为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为2的正方形MNEF的四个顶点分在大圆O上,小圆O与正方形各边都相切,AB与CD是大圆O的直径,AB⊥CD,CD⊥MN,小明随意向水平放置的该圆形区域内抛一个小球,则小球停在该图中阴影部分区域的概率为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据:
 ≈1.414,
≈1.414,  ≈1.732)
≈1.732)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的直径AB=4,∠BAC=30°,AC交⊙O于D,D是AC的中点.

(1)过点D作DE⊥BC,垂足为E,求证:直线DE是⊙O的切线;
(2)求 与线段DE、BE围成的阴影面积.
与线段DE、BE围成的阴影面积.
相关试题

