【题目】如图,⊙O的直径AB=4,∠BAC=30°,AC交⊙O于D,D是AC的中点. 
(1)过点D作DE⊥BC,垂足为E,求证:直线DE是⊙O的切线;
(2)求 ![]() 与线段DE、BE围成的阴影面积.
与线段DE、BE围成的阴影面积.
参考答案:
【答案】
(1)证明:连接OD.

∵D是AC的中点,O是AB的中点,
∴DO是△ABC的中位线,
∴OD∥BC,则∠EDO=∠CED
又∵DE⊥BC,
∴∠CED=90°,
∴∠EDO=∠CED=90°
∴OD⊥DE
∴DE是⊙O的切线,
(2)连接BD

∵AB是直径
∴∠ADB=90°
∵∠BAC=30°,AB=4
∴∠BOD=2∠ABD=60°
∵OB=OD
∴△OBD是等边三角形
∴∠ODB=∠BOD=60°,OB=OD=BD=2
∵∠EDO=90°
∴∠BDE=30°
∴在Rt△BDE中 BE=1,DE= ![]()
∴S阴=S四边形ODEB﹣S扇形OBD= ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]()
答:阴影面积为 ![]() ﹣
﹣ ![]()
【解析】(1)连接OD,易证DO是△ABC的中位线,从而可知OD∥BC,所以∠EDO=∠CED,由于DE⊥BC,从而可知DE是⊙O的切线;(2)连接BD,分别求出四边形OBED与扇形OBD的面积,然后即可求出阴影部分面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A1 , A2 , A3 , …,An是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1 , A2 , A3 , …,An+1作x轴的垂线交一次函数
 的图象于点B1 , B2 , B3 , …,Bn+1 , 连接A1B2 , B1A2 , A2B3 , B2A3 , …,AnBn+1 , BnAn+1依次产生交点P1 , P2 , P3 , …,Pn , 则Pn的坐标是 .
的图象于点B1 , B2 , B3 , …,Bn+1 , 连接A1B2 , B1A2 , A2B3 , B2A3 , …,AnBn+1 , BnAn+1依次产生交点P1 , P2 , P3 , …,Pn , 则Pn的坐标是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为2的正方形MNEF的四个顶点分在大圆O上,小圆O与正方形各边都相切,AB与CD是大圆O的直径,AB⊥CD,CD⊥MN,小明随意向水平放置的该圆形区域内抛一个小球,则小球停在该图中阴影部分区域的概率为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据:
 ≈1.414,
≈1.414,  ≈1.732)
≈1.732)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为丰富学生的校园生活,某校举行“与爱同行”朗诵比赛,赛后整理参赛同学的成绩,绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题.
组别
成绩x(分)
频数(人数)
A
8.0≤x<8.5
a
B
8.5≤x<9.0
8
C
9.0≤x<9.5
15
D
9.5≤x<10
3

(1)图中a= , 这次比赛成绩的众数落在组;
(2)请补全频数分布直方图;
(3)学校决定选派本次比赛成绩最好的3人参加全市中学生朗诵比赛,并为参赛选手准备了2件白色、1件蓝色上衣和黑色、蓝色、白色的裤子各1条,小军先选,他从中随机选取一件上衣和一条裤子搭配成一套衣服,请用画树状图法或列表法求出上衣和裤子搭配成不同颜色的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A是∠MON边OM上一点,AE∥ON.
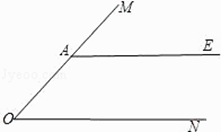
(1)在图中作∠MON的角平分线OB,交AE于点B;(要求:尺规作图,保留作图痕迹,不写作法和证明)
(2)在(1)中,过点A画OB的垂线,垂足为点D,交ON于点C,连接CB,将图形补充完整,并证明四边形OABC是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过A(1,0)、B(0,3)两点,对称轴是x=﹣1

(1)求抛物线对应的函数关系式;
(2)动点Q从点O出发,以每秒1个单位长度的速度在线段OM上运动,同时动点M从M从O点出发以每秒3个单位长度的速度在线段OB上运动,过点Q作x轴的垂线交线段AB于点N,交抛物线于点P,设运动的时间为t秒.
①当t为何值时,四边形OMPQ为矩形;
②△AON能否为等腰三角形?若能,直接写出t的值;若不能,请说明理由.
相关试题

