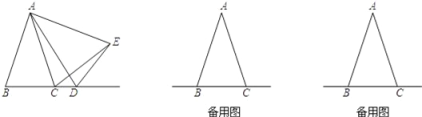
【题目】在△ABC中,AB=AC,D是线段BC的延长线上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
(1)如图1,点D在线段BC的延长线上移动,若∠BAC=30°,则∠DCE= .
(2)设∠BAC=α,∠DCE=β:
①如图1,当点D在线段BC的延长线上移动时,α与β之间有什么数量关系?请说明理由;
②当点D在直线BC上(不与B、C重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.
参考答案:
【答案】(1)30°;(2)①当点D在线段BC的延长线上移动时,α与β之间的数量关系是α=β;②当D在线段BC上时,α+β=180°,当点D在线段BC延长线或反向延长线上时,α=β.
【解析】
(1)证△BAD≌△CAE,推出∠B=∠ACE,根据三角形外角性质求出即可;
(2)①证△BAD≌△CAE,推出∠B=∠ACE,根据三角形外角性质求出即可;②分D在线段BC上时和当点D在线段BC延长线或反向延长线上时两种情况求解即可.
(1)解:(1)∵∠DAE=∠BAC,
∴∠DAE+∠CAD=∠BAC+∠CAD,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
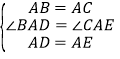 ,
,
∴△BAD≌△CAE(SAS),
∴∠B=∠ACE,
∵∠ACD=∠B+∠BAC=∠ACE+∠DCE,
∴∠BAC=∠DCE,
∵∠BAC=30°,
∴∠DCE=30°.
故答案为30;;
(2)①解:当点D在线段BC的延长线上移动时,α与β之间的数量关系是α=β,
理由是:
∵∠DAE=∠BAC,
∴∠DAE+∠CAD=∠BAC+∠CAD,
∴∠BAD=∠CAE,
在△BAD和△CAE中
∵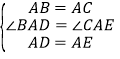 ,
,
∴△BAD≌△CAE(SAS),
∴∠B=∠ACE,
∵∠ACD=∠B+∠BAC=∠ACE+∠DCE,
∴∠BAC=∠DCE,
∵∠BAC=α,∠DCE=β,
∴α=β;
②解:当D在线段BC上时,α+β=180°,
理由如下:
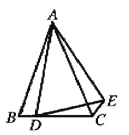
∵∠BAC=∠DAE,
∴∠BAD=∠CAE;
在△BAD与△CAE中,
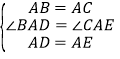 ,
,
∴△BAD≌△CAE(SAS),
∴∠B=∠ACE,
∴β=∠ABC+∠ACB,
∵∠ABC+∠ACB=180°-α,
∴α+β=180°.
故答案为α+β=180°;
当点D在线段BC延长线或反向延长线上时,α=β,证明如①.
∴当D在线段BC上时,α+β=180°,当点D在线段BC延长线或反向延长线上时,α=β.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市政府大力扶持大学生创业.张涛在政府的扶持下销售一种进价为每件20元的新型节能产品,现准备从国内和国外两种销售方案中选择一种进行销售.
若只在国内销售,销售价格y(元/件)与月销售量x(件)的函数关系如图所示.无论销售多少,每月还需支出广告费62500元,设月利润为W内(元)(利润=销售额-成本-广告费). 若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本(含进价)为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳
 x2元的附加费,设月利润为W外(元)(利润=销售额-成本-附加费).
x2元的附加费,设月利润为W外(元)(利润=销售额-成本-附加费).(1)求y与x的函数关系式(不必写x的取值范围);
(2)分别求出W内,W外与x间的函数关系式(不必写x的取值范围);
(3)在国内销售时,每月的销售量在什么范围内,张涛才不会亏本?
(4)如果某月要将5000件产品全部销售完,请你通过分析帮公司决策,选择在国内还是在国外销售才能使所获月利润较大?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C,D是AB的垂直平分线上两点,延长AC,DB交于点E,AF∥BC交DE于点F.
求证:(1)AB是∠CAF的角平分线;
(2)∠FAD = ∠E.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一个转盘被分成6个相等的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,重新转动).下列事件:①指针指向红色;②指针指向绿色;(③指针指向黄色;④指针不指向黄色,估计各事件的可能性大小,完成下列问题.
(1)④事件发生的可能性大小是 ;
(2)多次实验,指针指向绿色的频率的估计值是 ;
(3)将这些事件的序号按发生的可能性从小到大的顺序排列为:


 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①点O与O′的距离为4;②∠AOB=150°;③
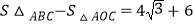 .其中正确的结论是( )
.其中正确的结论是( )
A. ①B. ①②C. ②③D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公交车每月的支出费用为4000元,每月的乘车人数
 (人)与每月利润(利润=收入费用-支出费用)
(人)与每月利润(利润=收入费用-支出费用) (元)的变化关系如下表所示(每位乘客的公交票价是固定不变的);
(元)的变化关系如下表所示(每位乘客的公交票价是固定不变的);
(1)在这个变化过程中, 是自变量, 是因变量;(填中文)
(2)观察表中数据可知,每月乘客量达到 人以上时,该公交车才不会亏损;
(3)请你估计当每月乘车人数为3500人时,每月利润为 元?
(4)若5月份想获得利润5000元,则请你估计5月份的乘客量需达 人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形
 (四边相等,四个角都是直角),点
(四边相等,四个角都是直角),点 为边
为边 上异于点
上异于点 的一动点,
的一动点, ,交
,交 于点
于点 ,点
,点 为
为 延长线上一定点,满足
延长线上一定点,满足 ,
, 的延长线与
的延长线与 交于点
交于点 ,连接
,连接 .
.(1)判断
 是 三角形.
是 三角形.(2)求证:
 ≌
≌ .
.(3)探究
 是否为定值?如果是定值,请说明理由,并求出该定值;如果不是定值,请说明理由.
是否为定值?如果是定值,请说明理由,并求出该定值;如果不是定值,请说明理由.
相关试题

