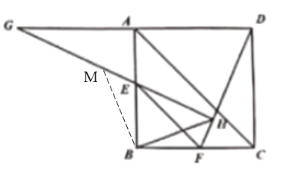
【题目】如图,已知正方形![]() (四边相等,四个角都是直角),点
(四边相等,四个角都是直角),点![]() 为边
为边![]() 上异于点
上异于点![]() 的一动点,
的一动点,![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 为
为![]() 延长线上一定点,满足
延长线上一定点,满足![]() ,
,![]() 的延长线与
的延长线与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
(1)判断![]() 是 三角形.
是 三角形.
(2)求证: ![]() ≌
≌![]() .
.
(3)探究![]() 是否为定值?如果是定值,请说明理由,并求出该定值;如果不是定值,请说明理由.
是否为定值?如果是定值,请说明理由,并求出该定值;如果不是定值,请说明理由.

参考答案:
【答案】(1)等腰直角;(2)证明见解析;(3)![]() ,为定值.
,为定值.
【解析】
(1)根据正方形性质证得∠BAC=∠BCA,然后再根据![]() 得出∠BEF=∠BAC,∠BFE=∠BCA,即可证得
得出∠BEF=∠BAC,∠BFE=∠BCA,即可证得![]() 是等腰直角三角形;
是等腰直角三角形;
(2)根据等腰直角三角形得出![]() ,然后求出四边形
,然后求出四边形![]() 为正方形,即可得出答案;
为正方形,即可得出答案;
(3)在![]() 上截取
上截取![]() ,根据(2)中的结论可求出
,根据(2)中的结论可求出![]() ,又因为
,又因为![]() ≌
≌![]() ≌
≌![]() ,
,![]() ,
,![]() ,所以证得
,所以证得![]() 为等腰直角三角形,得出
为等腰直角三角形,得出![]() .
.
解:(1) ∵四边形![]() 是正方形,AC为对角线,
是正方形,AC为对角线,
∴∠BAC=∠BCA,
又∵![]() ,
,
∴∠BEF=∠BAC,∠BFE=∠BCA,
则∠BEF=∠BFE,
∵正方形![]() 四个角为直角,
四个角为直角,
∴![]() 是等腰直角三角形;
是等腰直角三角形;
(2)∵![]() 和
和![]() 为等腰直角三角形
为等腰直角三角形
∴![]() ,
,
∴![]() ,即是
,即是![]() ,
,
∵四边形![]() 为正方形,
为正方形,
∴![]() ,
,![]() ,
,
∴![]() ≌
≌![]() (
(![]() );
);
(3)在![]() 上截取
上截取![]()
∵![]() ≌
≌![]()
∴![]()
∴![]()
即是![]()
∵![]() 为等腰直角三角形
为等腰直角三角形
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]() ≌
≌![]()
∴![]() ,
,![]()
∵![]()
∴![]() 即是
即是![]()
∴![]() 为等腰直角三角形,
为等腰直角三角形,![]() .
.
-
科目: 来源: 题型:
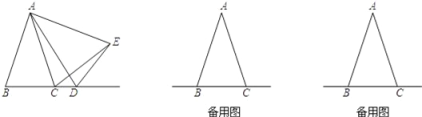
查看答案和解析>>【题目】在△ABC中,AB=AC,D是线段BC的延长线上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
(1)如图1,点D在线段BC的延长线上移动,若∠BAC=30°,则∠DCE= .
(2)设∠BAC=α,∠DCE=β:
①如图1,当点D在线段BC的延长线上移动时,α与β之间有什么数量关系?请说明理由;
②当点D在直线BC上(不与B、C重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①点O与O′的距离为4;②∠AOB=150°;③
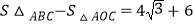 .其中正确的结论是( )
.其中正确的结论是( )
A. ①B. ①②C. ②③D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公交车每月的支出费用为4000元,每月的乘车人数
 (人)与每月利润(利润=收入费用-支出费用)
(人)与每月利润(利润=收入费用-支出费用) (元)的变化关系如下表所示(每位乘客的公交票价是固定不变的);
(元)的变化关系如下表所示(每位乘客的公交票价是固定不变的);
(1)在这个变化过程中, 是自变量, 是因变量;(填中文)
(2)观察表中数据可知,每月乘客量达到 人以上时,该公交车才不会亏损;
(3)请你估计当每月乘车人数为3500人时,每月利润为 元?
(4)若5月份想获得利润5000元,则请你估计5月份的乘客量需达 人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c﹣m=0没有实数根,有下列结论:①b2﹣4ac>0;②abc<0;③m<﹣3;④3a+b>0.其中,正确结论的个数是_________个.

-
科目: 来源: 题型:
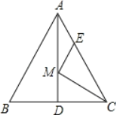
查看答案和解析>>【题目】如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点,若AE=2,EM+CM的最小值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图中小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点G为位似中心的位似图形,它们的顶点都在小正方形顶点上.
(1)画出位似中心点G;
(2)若点A、B在平面直角坐标系中的坐标分别为(﹣6,0),(-3,2),点P(m,n)是线段AC上任意一点,则点P在△A′B′C′上的对应点P′的坐标为 .

相关试题

