【题目】如图,在矩形![]() 中,
中,![]() 为对角线,过点
为对角线,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,
上,![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,
,![]() ,则线段
,则线段![]() 的长为______.
的长为______.
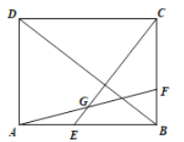
参考答案:
【答案】![]()
【解析】
连接AC交BD于O,BD交AF于M,连接GO,CM,CE交BD于点N.利用全等三角形的性质证明OC=CM,∠ACG=∠GCM,作GK⊥CM交CM的延长线于K,作GJ⊥AC于J.则有GJ=GK,可得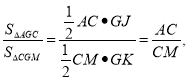
 推出AG=2GM,证明△MOG≌△MBF(AAS),可得OG=BF=GM=FM,设GM=k,则GM=BF=MF=OG=k,AG=FG=CF=2k,利用勾股定理构建方程组即可解决问题.
推出AG=2GM,证明△MOG≌△MBF(AAS),可得OG=BF=GM=FM,设GM=k,则GM=BF=MF=OG=k,AG=FG=CF=2k,利用勾股定理构建方程组即可解决问题.
解:连接AC交BD于O,BD交AF于M,连接GO,CM,CE交BD于点N.

∵四边形ABCD是矩形, ∴OA=OC,
∵AG=GF=CF, ∴∠FCG=∠FGC,OG∥CF,
∴∠OGC=∠FCG=∠FGC,
∵CE⊥BD, ∴∠GNO=∠GNM=90°,
∵GN=GN, ∴△GNO≌△GNM(ASA),
∴ON=NM,OG=GM,
∵∠CNO=∠CNM=90°,CN=CN,
∴△CNO≌△CNM(SAS),
∴∠OCN=∠MCN,OC=MC= ![]() AC,
AC,
∴GC平分∠ACM,作GK⊥CM交CM的延长线于K,作GJ⊥AC于J.则有GJ=GK,
∴ 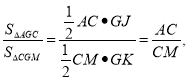
同理:
![]()
∴AG=2GM,
∵AG=GF, ∴GM=MF,
∵∠MOG=∠MBF,∠OMG=∠BMF,
∴△MOG≌△MBF(AAS),
∴OG=BF=GM=FM,
设GM=k,则GM=BF=MF=OG=k,AG=FG=CF=2k,
∴BC=3k,
在Rt△ABF中,∵![]() ∴
∴![]() ①,
①,
在Rt△ABC中,∵![]() AC=BD=
AC=BD= ![]()
∴![]() ②,
②,
由①②可得AB=![]()
故答案为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=3x2+1和y=3(x﹣1)2 , 以下说法: ①它们的图象都是开口向上;
②它们的对称轴都是y轴,顶点坐标都是原点(0,0);
③当x>0时,它们的函数值y都是随着x的增大而增大;
④它们的开口的大小是一样的.
其中正确的说法有( )
A. 1个 B. 2 C. 3 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=
 ,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )
,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )
A.
 B. 3 C. 2 D. 2
B. 3 C. 2 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=
 BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE= BC,成立的个数有( )
BC,成立的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AD=5,AB=3,点E,F在直线AD上,且四边形BCFE为菱形,若线段EF的中点为点M,则线段AM的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100 m,此时自B处测得建筑物顶部的仰部角是45°.已知测角仪的高度是1.5 m,请你计算出该建筑物的高度.(取≈1.732,结果精确到1 m)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用长为6m的铝合金条制成“日”字形窗框,若窗框的宽为xm,窗户的透光面积为ym2(铝合金条的宽度不计).
(1)求出y与x的函数关系式;
(2)如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.

相关试题

