【题目】在矩形ABCD中,AD=5,AB=3,点E,F在直线AD上,且四边形BCFE为菱形,若线段EF的中点为点M,则线段AM的长为 .
参考答案:
【答案】6.5,或1.5.
【解析】
试题分析:两种情况:①由矩形的性质得出CD=AB=3,BC=AD=5,∠ADB=∠CDF=90°,由菱形的性质得出CF=EF=BE=BC=5,由勾股定理求出DF,得出MF,即可求出AM;②同①得出AE=4,求出ME,即可得出AM的长.
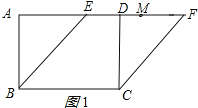
解:分两种情况:①如图1所示:
∵四边形ABCD是矩形,
∴CD=AB=3,BC=AD=5,∠ADB=∠CDF=90°,
∵四边形BCFE为菱形,
∴CF=EF=BE=BC=5,
∴DF=![]() =
=![]() =4,
=4,
∴AF=AD+DF=9,
∵M是EF的中点,
∴MF=![]() EF=2.5,
EF=2.5,
∴AM=AF﹣DF=9﹣2.5=6.5;
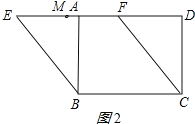
②如图2所示:同①得:AE=4,
∵M是EF的中点,
∴ME=2.5,
∴AM=AE﹣ME=1.5;
综上所述:线段AM的长为:6.5,或1.5;
故答案为:6.5,或1.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在|﹣2|,﹣|0|,(﹣2)5,﹣|﹣2|,+(﹣2)中,负数共有( )
A. 1 个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a<﹣1,点(a﹣1,y1),(a,y2),(a+1,y3)都在函数y=﹣x2的图象上,则( )
A.y1<y2<y3
B.y1<y3<y2
C.y3<y2<y1
D.y2<y1<y3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
 分别交
分别交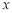 轴,
轴,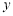 轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.
轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.(1)直接写出点A,B的坐标,并求直线AB与CD交点E的坐标;
(2)动点P从点C出发,沿线段CD以每秒1个单位长度的速度向终点D运动;同时,动点N从点A出发,沿线段AO以每秒1个单位长度的速度向终点O运动,过点P作
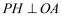 ,垂足为H,连接NP.设点P的运动时间为t秒.
,垂足为H,连接NP.设点P的运动时间为t秒.① 若△NPH的面积为1,求t的值;
② 点Q是点B关于点A的对称点,问
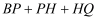 是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.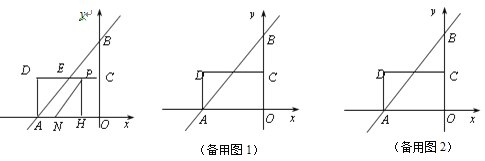
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,适合全面调查方式的是( )
A. 调查全国人民的环保意识 B. 调查中秋节期间市场月饼的质量
C. 调查某班40名同学的体重 D. 调查某类烟花爆炸燃放安全质量
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解我校八年级同学的视力情况,从八年级的15个班共590名学生中,每班随机抽取了5名进行分析。在这个问题中.样本是____________________,样本容量是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】⊙O为△ABC的外接圆,过圆外一点P作⊙O的切线PA,且PA∥BC.

(1)如图1,求证:△ABC为等腰三角形:
(2)如图2,在AB边上取一点E,AC边上取一点F,直线EF交PA于点M,交BC的延长线于点N,若ME=FN,求证:AE=CF;
(3)如图3,在(2)的条件下,连接OE、OF,∠EOF=120°,
 ,EF=
,EF= ,求⊙O的半径长.
,求⊙O的半径长.
相关试题

