【题目】如图,在等边△ABC中,线段AM为BC边上的中线.动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,连结BE.
(1)填空:∠CAM=__________度;
(2)若点D在线段AM上时,求证:△ADC≌△BEC;
(3)当动点D在直线AM上时,设直线BE与直线AM的交点为O,试判断∠AOB是否为定值?并说明理由.



参考答案:
【答案】30;
【解析】(1)根据等边三角形的性质可以直接得出结论;
(2)根据等边三角形的性质就可以得出AC=AC,DC=EC,∠ACB=∠DCE=60°,由等式的性质就可以∠BCE=∠ACD,根据SAS就可以得出△ADC≌△BEC;
(3)分情况讨论:当点D在线段AM上时,如图1,由(2)可知△ACD≌△BCE,就可以求出结论;当点D在线段AM的延长线上时,如图2,可以得出△ACD≌△BCE而有∠CBE=∠CAD=30°而得出结论;当点D在线段MA的延长线上时,如图3,通过得出△ACD≌△BCE同样可以得出结论.
解:(1)∵△ABC是等边三角形,
∴∠BAC=60°.
∵线段AM为BC边上的中线
∴∠CAM=![]() ∠BAC,
∠BAC,
∴∠CAM=30°.
故答案为:30;
(2)∵△ABC与△DEC都是等边三角形
∴AC=BC,CD=CE,∠ACB=∠DCE=60°
∴∠ACD+∠DCB=∠DCB+∠BCE
∴∠ACD=∠BCE.
在△ADC和△BEC中,AC=BC,∠ACD=∠BCE,CD=CE,,
∴△ACD≌△BCE(SAS);
(3)∠AOB是定值,∠AOB=60°,
理由如下:
①当点D在线段AM上时,如图1,

由(2)可知△ACD≌△BCE,则∠CBE=∠CAD=30°,
又∠ABC=60°
∴∠CBE+∠ABC=60°+30°=90°,
∵△ABC是等边三角形,线段AM为BC边上的中线
∴AM平分∠BAC,即∠BAM=![]() ∠BAC=
∠BAC=![]() ×60°=30°
×60°=30°
∴∠BOA=90°-30°=60°.
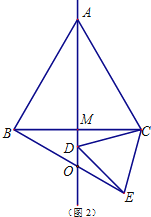
②当点D在线段AM的延长线上时,如图2,
∵△ABC与△DEC都是等边三角形
∴AC=BC,CD=CE,∠ACB=∠DCE=60°
∴∠ACB+∠DCB=∠DCB+∠DCE
∴∠ACD=∠BCE
在△ACD和△BCE中,AC=BC,∠ACD=∠BCE,CD=CE,
∴△ACD≌△BCE(SAS)
∴∠CBE=∠CAD=30°,
同理可得:∠BAM=30°,
∴∠BOA=90°-30°=60°.
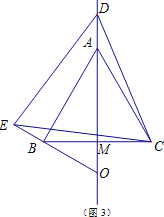
③当点D在线段MA的延长线上时,如图3,
∵△ABC与△DEC都是等边三角形
∴AC=BC,CD=CE,∠ACB=∠DCE=60°
∴∠ACD+∠ACE=∠BCE+∠ACE=60°
∴∠ACD=∠BCE
在△ACD和△BCE中,AC=BC,∠ACD=∠BCE,CD=CE,
∴△ACD≌△BCE(SAS)
∴∠CBE=∠CAD
同理可得:∠CAM=30°
∴∠CBE=∠CAD=150°
∴∠CBO=30°,∠BAM=30°,
∴∠BOA=90°-30°=60°.
综上,当动点D在直线AM上时,∠AOB是定值,∠AOB=60°.
“点睛”边三角形的性质的运用,直角三角形的性质的运用,等式的性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】你能很快算出19952吗?请按以下步骤表达探索过程(填空):
通过计算,探索规律:
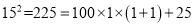 ,
, 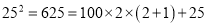 ,
, ,
, 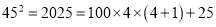
(1)
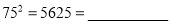 ,
,(2)从第(1)题的结果,归纳、猜想得
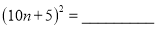
(3)请根据上面的归纳猜想,算出

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中错误的是( )
A.任意三角形的内角和都是180°
B.三角形按边分可分为不等边三角形和等腰三角形
C.三角形的中线、角平分线、高都是线段
D.三角形的一个外角大于任何一个内角 -
科目: 来源: 题型:
查看答案和解析>>【题目】规定:正整数n的“H运算”是:①当n为奇数时,H=3n+13;②当n为偶数时,H=n
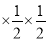 …(连续乘以
…(连续乘以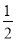 ,一直算到H为奇数止).如:数3经过“H运算”的结果是22,经过2次“H运算”的结果为11,经过三次“H运算”的结果为46,那么257经2017次“H运算”得到的结果是( )
,一直算到H为奇数止).如:数3经过“H运算”的结果是22,经过2次“H运算”的结果为11,经过三次“H运算”的结果为46,那么257经2017次“H运算”得到的结果是( )A. 161 B. 1 C. 16 D. 以上答案均不正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣16=0的解是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入相应的集合中:+2,-3,0,-3
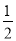 ,-1.414,-17,
,-1.414,-17, 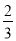 .
.负数:{____________________…};正整数:{__________________…};
整数:{___________________…}; 负分数:{___________________…};
分数:{__________________…}; 有理数:{__________________…}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的底角是顶角的2倍,则顶角的度数是__________.
相关试题

