【题目】计算
(1) (4a3b-6a2b2+12ab3)÷2ab
(2) a3·a4·a+(a2)4+(-2a4)2
(3) ![]()
(4)![]()
(5)![]()
参考答案:
【答案】(1)2a2-3ab+6b2;(2)6a8;(3)3x2-4xy-5y2;(4)x2-11x+6;(5)![]()
【解析】
(1)根据多项式除以单项式法则计算可得;
(2)根据先根据同底数幂乘法、幂的乘方、积的乘方法则计算;再合并同类项即可;
(3)根据先利用平方差公式和完全平方公式计算,再进行加减运算可得.
(4)根据单项式、多项式乘以多项式的运算法则计算可得;
(5)原式先利用零指数幂、负整数指数幂等法则计算乘方运算,再有理数加减运算即可得到结果;
解:(1) (4a3b-6a2b2+12ab3)÷2ab,
=2a2-3ab+6b2;
(2) a3·a4·a+(a2)4+(-2a4)2,
=![]() ,
,
=![]() ,
,
=![]() ;
;
(3) ![]() ,
,
=![]() ,
,
=![]() ,
,
=![]() ;
;
(4)![]() ,
,
=![]() ,
,
=![]() ,
,
=![]()
(5)![]()
=1-![]() +9-4
+9-4
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解本校中考体育备考情况,随机抽去九年级部分学生进行了一次测试(满分60分,成绩均记为整数分)并按测试成绩(单位:分)分成四类:A类(54≤a≤60),B类(48≤a≤53),C类(36≤a≤47),D类(a≤35)绘制出如下两幅不完整的统计图,请根据图中信息,解答下列问题:

(1)请补全统计图;
(2)在扇形统计图汇总,表示成绩类别为“C”的扇形所对应的圆心角是________度;
(3)该校准备召开体育考经验交流会,已知A类学生中有4人满分(男生女生各有2人),现计划从这4人中随机选出2名学生进行经验介绍,请用树状图或列表法求所抽到的2,名学生恰好是一男一女的概率
-
科目: 来源: 题型:
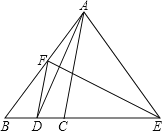
查看答案和解析>>【题目】如图,在△ABC中,AD是∠BAC的平分线,AD的垂线平分线交AB于点F,交BC的延长线于点E,连接AE,DF.
求证:(1)∠EAD=∠EDA;(2)DF//AC;(3)∠EAC=∠B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了创建书香校园,今年又购进一批图书,经了解,科普书的单价比文学书的单价多4元,用1200元购进的科普书与用800元购进的文学书本数相等.
(1)今年购进的文学书和科普书的单价各是多少元?
(2)该校购买这两种书共180本,总费用不超过2000元,且购买文学书的数量不多于42本,应选择哪种购买方案可使总费用最低?最低费用是多少元?
-
科目: 来源: 题型:
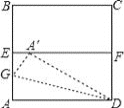
查看答案和解析>>【题目】如图,ABCD是一张边长为4cm的正方形纸片,E,F分别为AB,CD的中点,沿过点D的折痕将A 角翻折,使得点A落在EF上的点A′处,折痕交AE于点G,则EG=_________cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图中提供的信息,有下列说法:①两人相遇前,甲的速度小于乙的速度;②出发后1小时,两人行程均为10km;③出发后1.5小时,甲的行程比乙少3km;④甲比乙先到达终点.其中正确的有( )

A.4个B.3个C.2个D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.

(1)求抛物线的函数解析式.
(2)设点D在抛物线上,点E在抛物线的对称轴上,若四边形AODE是平行四边形,求点D的坐标.
(3)联接BC交x轴于点F.y轴上是否存在点P,使得△POC与△BOF相似?若存在,求出点P的坐标;若不存在,请说明理由.
相关试题

