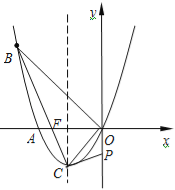
【题目】如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.

(1)求抛物线的函数解析式.
(2)设点D在抛物线上,点E在抛物线的对称轴上,若四边形AODE是平行四边形,求点D的坐标.
(3)联接BC交x轴于点F.y轴上是否存在点P,使得△POC与△BOF相似?若存在,求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1) y=x2+2x;(2) (1,3);(3) (0,﹣ ![]() )或(0,﹣4).
)或(0,﹣4).
【解析】试题分析:(1)将点A、点B和原点代入解析式进行求解;(2)根据平行四边形的性质得出点D的坐标;(3)首先求出OB、OF、OC的长度,然后根据三角形相似的条件求出点P的坐标,分两种情况进行讨论.
试题解析:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),
将点A(﹣2,0),B(﹣3,3),O(0,0),代入可得: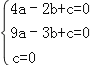 ,解得:
,解得:![]() ,
,
所以函数解析式为:y=x2+2x;
(2)∵AO为平行四边形的一边, ∴DE∥AO,DE=AO, ∵A(﹣2,0),
∴DE=AO=2, ∵四边形AODE是平行四边形, ∴D在对称轴直线x=﹣1右侧,
∴D横坐标为:﹣1+2=1,代入抛物线解析式得y=3, ∴D的坐标为(1,3);
(3)在y轴上存在点P,使得△POC与△BOF相似,理由如下:
由y=x2+2x,顶点C的坐标为(﹣1,1) ∵tan∠BOF=![]() ,
,
∴∠BOF=45°, 当点P在y轴的负半轴时,tan∠COP=![]() ,
,
∴∠COP=45°,∴∠BOF=∠COP, 设BC的解析式为y=kx+b(k≠0),
∵图象经过B(﹣3,3),C(﹣1,1)
∴![]() , 解得∴
, 解得∴![]() ,
,
∴y=﹣2x﹣3; 令y=0,则x=﹣1.5.
∴F(﹣1.5,0),
∴OB=3![]() ,OF=1.5,OC=
,OF=1.5,OC=![]() ,
,
①当△POC∽△FOB时, 则![]() ,
,
即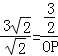 , ∴OP=
, ∴OP=![]() , ∴P(0,﹣
, ∴P(0,﹣![]() )
)
②当△POC∽△BOF时, ∴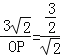 ,
,
∴OP=4, ∴P(0,﹣4),
∴当△POC与△BOF相似时,点P的坐标为(0,﹣![]() )或(0,﹣4).
)或(0,﹣4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1) (4a3b-6a2b2+12ab3)÷2ab
(2) a3·a4·a+(a2)4+(-2a4)2
(3)
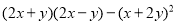
(4)
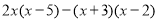
(5)
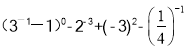
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD是一张边长为4cm的正方形纸片,E,F分别为AB,CD的中点,沿过点D的折痕将A 角翻折,使得点A落在EF上的点A′处,折痕交AE于点G,则EG=_________cm.
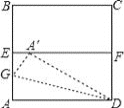
-
科目: 来源: 题型:
查看答案和解析>>【题目】在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图中提供的信息,有下列说法:①两人相遇前,甲的速度小于乙的速度;②出发后1小时,两人行程均为10km;③出发后1.5小时,甲的行程比乙少3km;④甲比乙先到达终点.其中正确的有( )

A.4个B.3个C.2个D.1个
-
科目: 来源: 题型:
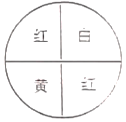
查看答案和解析>>【题目】如图,小华蒙上眼睛投飞镖且中目标(转盘技等分成4个扇形,投在边线上忽略)(直接填写答案)
(1)击中红色区域的概率是 .
(2)击中白色区域的概率是 .
(3)没有击中黄色区域的概率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】初二年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初二学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:
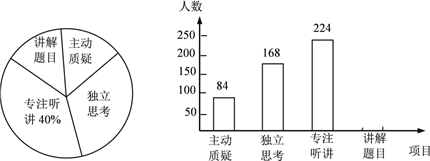
(1)在这次评价中,一共抽查了 名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为 度;
(3)请将频数分布直方图补充完整;
(4)如果全市有6000名初二学生,那么在试卷评讲课中,“独立思考”的初二学生约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知平行四边形ABCD的两条对角线相交于点O,E是BO的中点,过B点作AC的平行线,交CE的延长线于点F,连接BF。
(1)求证:FB=AO;
(2)平行四边形ABCD满足什么条件时,四边形AFBO是矩形?说明理由.

相关试题

