【题目】几何计算:
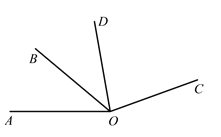
如图,已知∠AOB=40°,∠BOC=3∠AOB,OD平分∠AOC,求∠COD的度数.
解:因为∠BOC=3∠AOB,∠AOB=40°
所以∠BOC=__________°
所以∠AOC=__________ + _________
=__________° + __________°
=__________°
因为OD平分∠AOC
所以∠COD=![]() __________=__________°
__________=__________°

参考答案:
【答案】答案见解析.
【解析】试题分析:利用角倍数关系先求出∠BOC,再求出∠AOC,最后利用角平分线可知∠COD.
试题解析:
解:因为∠BOC=3∠AOB,∠AOB=40°,
所以∠BOC=__120__°,
所以∠AOC=_∠AOB_ + __∠BOC__,
=____40___° + ___120___°,
=___160___°,
因为OD平分∠AOC,
所以∠COD=![]() __∠AOC__=___80___°.
__∠AOC__=___80___°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知2x=3,2y=5,求2x+y的值;
(2)x﹣2y+1=0,求:2x÷4y×8的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,AB=2.
(1)尺规作图(保留作图痕迹,不写作法):作⊙O的内接正六边形ACDBEF。
(2)在(1)的条件下,直线PE与⊙O相切于点E,交AB延长线于点P,求PB、PE和
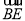 所围成的图形面积。
所围成的图形面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子中装有3个形状大小完全一样的小球,上面分别有标号1,2,-1,用树状图或列表的方法解决下列问题:
(1)将球搅匀,从盒中一次取出两个球,求其两标号互为相反数的概率。
(2)将球搅匀,摸出一个球将其标号记为k,放回后搅匀后再摸出一个球,将其标号记为b.求直线y=kx+b不经过第三象限的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以lcm/s的速度运动,同时点F从点B出发沿线射BC以2cm/s的速度运动,设运动时间为t(s).
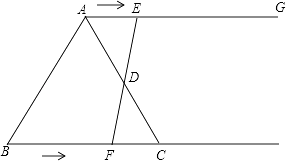
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)当t为多少时,四边形ACFE是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】比较2100与375的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1, 在△ABC中,∠C=90°,AC=9cm,动点P从点A以1cm/s的速度沿AB向点B运动,运动到点B终止,同时动点Q从点B沿BA向点A匀速运动,运动到点A终止。设运动时间为x(s),P、Q之间的距离为y(cm),且y与x的函数图象如图2所示。
(1)动点Q的运动速度为 。
(2)点N所表示的实际意义是 。
(3)若△PQC的面积为18cm2,求运动的时间x

相关试题

