【题目】如图1, 在△ABC中,∠C=90°,AC=9cm,动点P从点A以1cm/s的速度沿AB向点B运动,运动到点B终止,同时动点Q从点B沿BA向点A匀速运动,运动到点A终止。设运动时间为x(s),P、Q之间的距离为y(cm),且y与x的函数图象如图2所示。
(1)动点Q的运动速度为 。
(2)点N所表示的实际意义是 。
(3)若△PQC的面积为18cm2,求运动的时间x

参考答案:
【答案】(1)2cm/s;(2)点P、Q运动5s时相遇;(3)当运动时间为![]() s或
s或![]() s。时
s。时![]() .
.
【解析】(1)由图象可知AB长为15cm,P、Q同时出发,5s相遇,P运动速度为1cm每秒,可得Q点运动速度;(2)由图象得P、Q相距为0,则说明点P、Q运动5s时相遇;(3)
本题解析:(1)2cm/s;
(2)点P、Q运动5s时相遇
(3)作CD⊥AB,
由函数图象可知AB=15
又 ∠C=90°,AC=9cm, BC=12cm
∵AC·BC=AB·CD, ∴CD=7.2cm ,∵![]() ,∴
,∴![]()
∴PQ=5 , 又∵![]() ,(0≤x≤5) 即
,(0≤x≤5) 即![]() ,x=
,x=![]()
∴![]() 即x=
即x=![]()
∴当运动时间为![]() s或
s或![]() s。时
s。时![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】几何计算:
如图,已知∠AOB=40°,∠BOC=3∠AOB,OD平分∠AOC,求∠COD的度数.
解:因为∠BOC=3∠AOB,∠AOB=40°
所以∠BOC=__________°
所以∠AOC=__________ + _________
=__________° + __________°
=__________°
因为OD平分∠AOC
所以∠COD=
 __________=__________°
__________=__________°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以lcm/s的速度运动,同时点F从点B出发沿线射BC以2cm/s的速度运动,设运动时间为t(s).
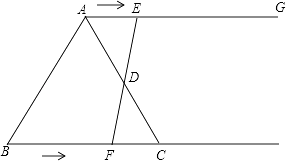
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)当t为多少时,四边形ACFE是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】比较2100与375的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)阅读理解:实数
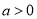 ,
, 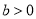 ,∵
,∵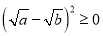 ,∴
,∴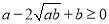 ,即
,即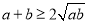 。若
。若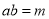 (
(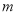 为定值),则
为定值),则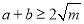 ,当且仅当
,当且仅当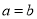 时等式成立,即
时等式成立,即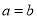 时,
时, 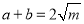 ,∴当
,∴当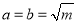 时,
时, 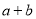 取得 值(填“最大”或“最小”)。
取得 值(填“最大”或“最小”)。(2)理解应用:函数
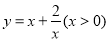 ,当x= 时,
,当x= 时, 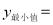 。
。(3)拓展应用:如图,双曲线
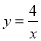 经过矩形OABC的对角线交点P,求矩形OABC的最小周长。
经过矩形OABC的对角线交点P,求矩形OABC的最小周长。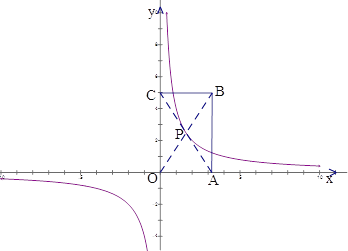
-
科目: 来源: 题型:
查看答案和解析>>【题目】小红同学要测量A、C两地的距离,但A、C之间有一水池,不能直接测量,于是她在A、C同一水平面上选取了一点B,点B可直接到达A、C两地.她测量得到AB=80米,BC=20米,∠ABC=120°.请你帮助小红同学求出A、C两点之间的距离.(参考数据
 ≈4.6)
≈4.6) -
科目: 来源: 题型:
查看答案和解析>>【题目】在儿时玩玩具手枪,在瞄准时总是半闭着眼,对着准星与目标,用数学知识解释为 .
相关试题

