【题目】已知函数![]()
(1)若函数图像经过原点,求m的值;
(2)若这个函数是一次函数,且与y轴交点为(0,3),求该一次函数图像与两坐标轴围成的三角形的周长.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)将(0,0)代入一次函数解析式中即可得出关于m的一元一次方程,解之即可得出结论;
(2)将(0,3)代入一次函数解析式中即可求出m,得到一次函数的解析式,从而求出其与x轴的交点.再根据勾股定理得到与坐标轴围成的直角三角形的斜边长,从而求得周长.
解:(1)∵函数![]() 的图象经过原点,
的图象经过原点,
∴0=m+3,
∴m=-3.
(2)∵函数![]() 是一次函数,且与y轴交点为(0,3),
是一次函数,且与y轴交点为(0,3),
得到![]() ,
,
解得:![]() ,
,
∴一次函数解析式为:y=-x+3,
当y=-x+3=0时,x=3,
∴一次函数y=-x+3与x轴交点为(3,0),
∴一次函数图像与两坐标轴围成的三角形的周长为:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究:
如图,抛物线y=
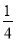 x2﹣
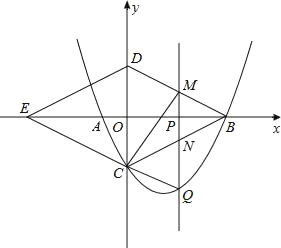
x2﹣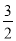 x﹣4与x轴交与A,B两点(点B在点A的右侧),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
x﹣4与x轴交与A,B两点(点B在点A的右侧),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.(1)求点A,B,C的坐标.
(2)当点P在线段OB上运动时,直线l分别交BD,BC于点M,N.试探究m为何值时,四边形CQMD是平行四边形,此时,请判断四边形CQBM的形状,并说明理由.
(3)当点P在线段EB上运动时,是否存在点Q,使△BDQ为直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B两地有公路和铁路相连,在这条路上有一家食品厂,它到B地的距离是到A地的2倍,这家厂从A地购买原料,制成食品卖到B地.已知公路运价为1.5元/(公里吨),铁路运价为1元/(公里吨),这两次运输(第一次:A地→食品厂,第二次:食品厂→B地)共支出公路运费15600元,铁路运费20600元.
问:(1)这家食品厂到A地的距离是多少?
(2)这家食品厂此次买进的原料每吨5000元,卖出的食品每吨10000元,此批食品销售完后工厂共获利多少元?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(0,a),B(b,a),且a,b满足(a﹣3)2+|b﹣6|=0,现同时将点A,B分别向下平移3个单位,再向左平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.

(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD;
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=
 S四边形ABCD?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
S四边形ABCD?若存在这样一点,求出点M的坐标,若不存在,试说明理由;(3)点P是直线BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合),直接写出∠BAP,∠DOP,∠APO之间满足的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点
 、
、 、
、 不在同一条直线上,
不在同一条直线上, .
.
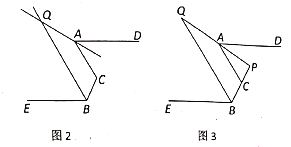
(1)如图1,当
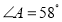 ,
, 时,求
时,求 的度数;
的度数;(2)如图2,
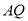 、
、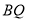 分别为
分别为 、
、 的平分线所在直线,试探究
的平分线所在直线,试探究 与
与 的数量关系;
的数量关系;(3)如图3,在(2)的前提下,有
 ,
, ,直接写出
,直接写出 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:A+2B=
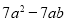 ,B=
,B=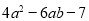 .
.(1)求A;
(2)若
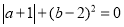 计算A的值.
计算A的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)(观察思考):如图,线段AB上有两个点C、D,图中共有 条线段;

(2)(模型构建):如果线段上有m个点(包括线段的两个端点),则该线段上共有 条线段.请简要说明结论的正确性;
(3)(拓展应用):8位同学参加班上组织的象棋比赛,比赛采用单循环制(即每两位同学之间都要进行一场比赛),那么一共要进行 场比赛.类比(模型构建)简要说明.
相关试题

