搜索
【题目】计算：（ 
）﹣1+（3﹣π）°﹣|1﹣tan60°|+ 
÷2．
参考答案：
【答案】解：原式=2+1﹣ 
+1+ =4
【解析】原式利用零指数幂、负整数指数幂法则，绝对值的代数意义，以及二次根式性质计算即可得到结果．
【考点精析】关于本题考查的整数指数幂的运算性质和特殊角的三角函数值，需要了解aman=am+n(m、n是正整数)；（am）n=amn(m、n是正整数)；(ab)n=anbn(n是正整数)；am/an=am-n(a不等于0，m、n为正整数）；（a/b）n=an/bn(n为正整数)；分母口诀：30度、45度、60度的正弦值、余弦值的分母都是2，30度、45度、60度的正切值、余切值的分母都是3，分子口诀：“123，321，三九二十七”才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算．
(1)( x-y)7÷(y-x)2÷( x-y)3；
(2)
+
+
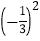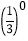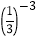；(3)( -2)0-
+
+
·
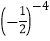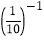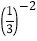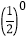；(4) a4m+1÷(-a) 2m+1 (m为正整数)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我们给出如下定义：顺次连接任意一个四边形各边中点所得的四边形叫中点四边形．
（1）如图1，四边形ABCD中，点E，F，G，H分别为边AB，BC，CD，DA的中点．求证：中点四边形EFGH是平行四边形；
（2）如图2，点P是四边形ABCD内一点，且满足PA=PB，PC=PD，∠APB=∠CPD，点E，F，G，H分别为边AB，BC，CD，DA的中点，猜想中点四边形EFGH的形状，并证明你的猜想；
（3）若改变（2）中的条件，使∠APB=∠CPD=90°，其他条件不变，直接写出中点四边形EFGH的形状．（不必证明）
-
科目： 来源： 题型：
查看答案和解析>>【题目】定义新运算：对于任意实数a，b，都有a⊕b=a（a﹣b）+1，等式右边是通常的加法，减法及乘法运算．比如：2⊕5=2×（2﹣5）+1=2×（﹣3）+1=﹣6+1=﹣5
（1）求3⊕（﹣2）的值；
（2）若3⊕x的值小于16，求x的取值范围，并在数轴上表示出来．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD中，点E在对角线AC上，点F在边BC上，连接BE、DF，DF交对角线AC于点G，且DE=DG．
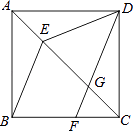
（1）求证：AE=CG；
（2）试判断BE和DF的位置关系，并说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】学校准备在各班设立图书角以丰富同学们的课余文化生活，为了更合理的搭配各类书籍，学校团委以“我最喜爱的书籍”为主题，对学生最喜爱的一种书籍类型进行随机抽样调查，收集整理数据后，绘制出以下两幅未完成的统计图，请根据图1和图2提供的信息，解答下列问题：
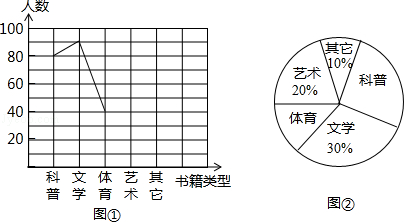
（1）在这次抽样调查中，一共调查了多少名学生？
（2）请把折线统计图（图1）补充完整；
（3）求出扇形统计图（图2）中，体育部分所对应的圆心角的度数；
（4）如果这所中学共有学生1800名，那么请你估计最喜爱科普类书籍的学生人数．
（5）学校若在喜爱艺术、文学、科普、体育四类中任意抽取两类建立兴趣小组，求出恰好选中是体育和科普两类的概率？ -
科目： 来源： 题型：
查看答案和解析>>【题目】已知，在
中，
，分别过
、
点作互相平行的直线
、
，过点
的直线分别交直线、于点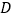
、
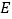.（1）
；① 若
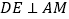，直接写出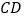
、
的数量关系；② 如图1，
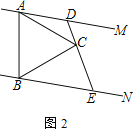
与不垂直，判断上述结论是否还成立，并说明理由；（2）如图2，
，
，
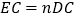，求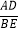
.
相关试题
