【题目】如图,在直角梯形ABCD中,AD⊥DC,AB∥DC,AB=BC,AD与BC延长线交于点F,G是DC延长线上一点,AG⊥BC于E,
(1)求证:CF=CG;
(2)连接DE,若BE=4CE,CD=2求DE的长.

参考答案:
【答案】(1)证明见解析;(2)DE=![]()
【解析】分析:(1)连接AC,首先可通过DG∥AB,AB=BC证得AC为∠DCE的角平分线,从而得到△ADC≌△AEC,可知CD=CE;再由∠FDC=∠GEC=90°,∠FCD=∠GCE,可判定△FDC≌△GEC,即可得CF=CG.(2)由已知条件,可求得AE、AC的长,法一:可利用C、A分别是DE垂直平分线上的点,并通过解直角三角形AEC的面积求得EH的长,从而得到ED的长.法二:通过证明△ADE∽△BAC可得![]() ,从而求得DE的长.
,从而求得DE的长.
本题解析:
(1)证明:连接AC

∵DC∥AB,AB=BC, ∴∠1=∠CAB, ∠CAB=∠2,
∴∠1=∠2,∠ADC=∠AEC=90°,AC=AC,
∴△ADC≌△AEC,∴CD=CE
∵∠FDC=∠GEC=90°, ∠3=∠4, ∴△FDC≌△GEC,
∴CF=CG,
(2)解:由(1)知,CE=CD=2,∴BE=4CE=8,∴AB=BC=CE+BE=10,
∴在RT△ABE中,AE=![]() ,
,
∴在RT△ACE中,AC=![]() ,
,
法一:由(1)知,△ADC≌△AEC,∴CD=CE,AD=AE,
∴C、A分别是DE垂直平分线上的点,
∴DE⊥AC,DE=2EH,
在RT△AEC中, ![]() ,
,
∴![]() ,
,
∴DE=2EH=2×![]() .
.
法二:在RT△AEC中,∠2+∠6=90°,
在RT△AEH中,∠5+∠6=90°,∴∠2=∠5,
∵AD=AE,AB=BC, ∴∠5=∠7,∠CAB=∠2
∴∠7=∠CAB,∴△ADE∽△BAC,
∴![]() , 即
, 即![]() ,
,
∴DE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠AOB=90,∠BOC=40,则∠AOB的平分线与∠BOC 的平分线的夹角等于( )
A.65
B.25
C.65或25
D.60或20 -
科目: 来源: 题型:
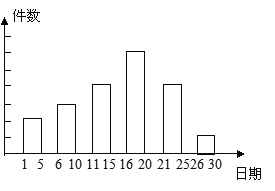
查看答案和解析>>【题目】在我校举办的课外活动中,有一项是小制作评比.作品上交时限为3月1日至30日,组委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1. 第三组的件数是12件. 请你回答:
(1)本次活动共有________件作品参赛;各组作品件数的中位数是________件.
(2)经评比,第四组和第六组分别有10件和2件作品获奖,那么你认为这两组中哪个组获奖率较高?为什么?
小制作评比结束后,组委会决定从4件最优秀的作品A、B、C、D中选出两件进行全校展示,请用树状图或列表法求出刚好展示B、D的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】实数a、b在数轴上的位置如图所示,下列各式成立的是( )

A.
B.a﹣b>0
C.ab>0
D.a+b>0 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中错误的是( )
A.既是矩形又是菱形的四边形是正方形B.有一个角是直角的菱形是正方形
C.有一组邻边相等的矩形是正方形D.对角线互相垂直平分的四边形是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式组
 的解集在数轴上表示为( )
的解集在数轴上表示为( )
A.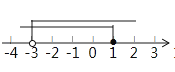
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,若AB∥DE,∠B=135°,∠D=145°,你能求出∠C的度数吗?
(2)在AB∥DE的条件下,你能得出∠B、∠C、∠D之间的数量关系吗?并说明理由.

相关试题

