【题目】若∠AOB=90,∠BOC=40,则∠AOB的平分线与∠BOC 的平分线的夹角等于( )
A.65
B.25
C.65或25
D.60或20
参考答案:
【答案】C
【解析】本题应分两种情况讨论:(1)当OC在∠AOB内部;(2)当OC在∠AOB外部,根据角平分线的性质及角的和差关系求解即可。
(1)当OC在∠AOB内部时,
∵∠AOB=90°,∠BOC=40°,OD,OE是∠AOB的与∠BOC的平分线,
∴∠AOD=∠DOB=![]() ∠AOB=45°,∠BOE=∠EOC=
∠AOB=45°,∠BOE=∠EOC=![]() ∠BOC=20°,
∠BOC=20°,
∴∠DOE=∠DOB-∠EOB=45°-20°=25°;
(2)当OC在∠AOB外部时,
∵∠AOB=90°,∠BOC=40°,OD,OE是∠AOB的与∠BOC的平分线,
∴∠AOD=∠DOB=![]() ∠AOB=45°,∠BOE=∠EOC=
∠AOB=45°,∠BOE=∠EOC=![]() ∠BOC=20°,
∠BOC=20°,
∴∠DOE=∠DOB+∠EOB=45°+20°=65°;
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+2x﹣(m﹣2)=0有实数根,则m的取值范围是( )
A.m>1
B.m<1
C.m≥1
D.m≤1 -
科目: 来源: 题型:
查看答案和解析>>【题目】为推进节能减排,发展低碳经济,某市“用电大户”用480万元购得“变频调速技术”后,进一步投入资金1520万元购买配套设备,以提高用电效率达到节约用电的目的.已知该“用电大户”生产的产品“草甘磷”每件成本费为40元.经过市场调研发现:该产品的销售单价,需定在100元到300元之间较为合理.当销售单价定为100元时,年销售量为20万件;当销售单价超过100元,但不超过200元时,每件新产品的销售价格每增加10元,年销售量将减少0.8万件;当销售单价超过200元,但不超过300元时,每件产品的销售价格在200元的基础上每增加10元,年销售量将减少1万件.设销售单价为x(元),年销售量为y(万件),年获利为w(万元).(年获利=年销售额-生产成本-节电投资)
(1)直接写出y与x之间的函数关系式;
(2)求第一年的年获利w与x间的函数关系式,并说明投资的第一年,该“用电大户”是盈利还是亏损?若盈利,最大利润是多少?若亏损,最少亏损是多少?
(3)若该“用电大户”把“草甘磷”的销售单价定在超过100元,但不超过200元的范围内,并希望到第二年底,除去第一年的最大盈利(或最小亏损)后,两年的总盈利为1842万元,请你确定此时销售单价.在此情况下,要使产品销售量最大,销售单价应定为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】钓鱼岛自古就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测。一日,中国一艘海监船从A点沿正北方向巡航,其航线距钓鱼岛(设M、N为该岛的东西两端点)最近距离为14km(即MC=14km)。在A点测得岛屿的西端点M在点A的东北方向;航行4km后到达B点,测得岛屿的东端点N在点B的北偏东60°方向(其中N、M、C在同一条直线上),求钓鱼岛东西两端点M、N之间的距离(结果保留根号)。

-
科目: 来源: 题型:
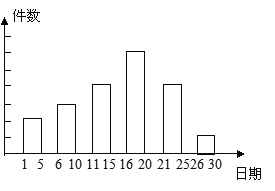
查看答案和解析>>【题目】在我校举办的课外活动中,有一项是小制作评比.作品上交时限为3月1日至30日,组委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1. 第三组的件数是12件. 请你回答:
(1)本次活动共有________件作品参赛;各组作品件数的中位数是________件.
(2)经评比,第四组和第六组分别有10件和2件作品获奖,那么你认为这两组中哪个组获奖率较高?为什么?
小制作评比结束后,组委会决定从4件最优秀的作品A、B、C、D中选出两件进行全校展示,请用树状图或列表法求出刚好展示B、D的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】实数a、b在数轴上的位置如图所示,下列各式成立的是( )

A.
B.a﹣b>0
C.ab>0
D.a+b>0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中,AD⊥DC,AB∥DC,AB=BC,AD与BC延长线交于点F,G是DC延长线上一点,AG⊥BC于E,
(1)求证:CF=CG;
(2)连接DE,若BE=4CE,CD=2求DE的长.

相关试题

